In this section we are going to cover the key components of valuation, and effectively set up the valuation worksheet. Based upon the cash flow statement, Free Cash Flow = operating activities – capital expenditures.
Terms:
Equity: looking at the share price in consideration of buying or selling shares and/or looking at the company’s equity as a whole when looking at acquiring the company.
Debt: when the company’s liabilities are substantial, this factors into a lower valuation based on higher risk. The formal way of calculating this is to subtract the sum of cash and short-term investments from short-term debt and current portion of long-term debt.
Cost of Debt: interest expense/debt.
WACC: weighted average cost of capital: Debt and equity are proportionally weighted in determining the cost of capital, and ultimately risk. The higher the WACC, the higher the risk.
\[\begin{eqnarray}
\text{$WACC$} &=& \frac{E}{V}R_e + \frac{D}{V}R_d(1-T_c)\\
\\
R_e &=& \text{cost of equity}\\
R_d &=& \text{cost of debt}\\
E &=& \text{market value of the firm's equity}\\
D &=& \text{market value of the firm's debt}\\
V &=& E+D \text{ = total market value of the firm’s financing (equity and debt)}\\
E/V &=& \text{percentage of financing that is equity}\\
D/V &=& \text{percentage of financing that is debt}\\
T_c &=& \text{corporate tax rate}
\\
\end{eqnarray}\]
\(\textbf{Enterprise Value}\)
\[\begin{eqnarray}
EV &=& \Large \sum_{t=1}^N \normalsize \frac{FCF_t}{(1+WACC)^t} \longrightarrow \frac{\text{free cash flow at time }t}{\text{(1 + weighted average cost of capital)}^t}\\
\\
\textcolor{red}{\text{where $WACC$}} &\textcolor{red}{=}& \textcolor{red}{\text{discount rate}}\\
\\
&=& \Large \sum_{t=1}^N \normalsize \frac{FCF_t}{(1+WACC)^{t-0.5}} + \normalsize \frac{\text{Terminal Value}}{(1+WACC)^{N-0.5}}\\
\\
&=& \Large \sum_{t=1}^N \normalsize \frac{FCF_t}{(1+\textcolor{red}{\frac{E}{V}R_e + \frac{D}{V}R_d(1-T_c)})^{t-0.5}} +
\normalsize \frac{\text{Terminal Value}}{(1+\textcolor{red}{\frac{E}{V}R_e + \frac{D}{V}R_d(1-T_c)})^{N-0.5}}\\
\\
\textcolor{red}{\text{where $WACC$}} &\textcolor{red}{=}& \textcolor{red}{\frac{E}{V}R_e + \frac{D}{V}R_d(1-T_c)} \textcolor{red} {\text{ and}}\\
\\
\textcolor{red}{\text{$V$}} &\textcolor{red}{=}& \textcolor{red}{(E+D) = \text{Equity + Debt}}\\
\\
& &\text{Rearranging the terms gives us the following:}& &\\
\\
&=& \left[ \Large \sum_{t=1}^N \normalsize \frac{FCF_t}{(1+WACC)^t} + \normalsize \frac{\text{Terminal Value}}{(1+WACC)^N} \right](1+WACC)^{0.5}\\
\\
&=& \left[ \Large \sum_{t=1}^N \normalsize \frac{FCF_t}{(1+\textcolor{red}{\frac{E}{V}R_e + \frac{D}{V}R_d(1-T_c)})^t} + \normalsize \frac{\text{Terminal Value}}{(1+\textcolor{red}{\frac{E}{V}R_e + \frac{D}{V}R_d(1-T_c)})^N} \right]\\
\\
& &\large \left [\normalsize \frac{(1+\textcolor{red}{\frac{E}{V}R_e + \normalsize \frac{D}{V}R_d(1-T_c)})^{0.5}}{1} \large \right]\\
\end{eqnarray}\]
Example 1
Equity (x) market cap.
This is the share price (x) shares outstanding.
=23.8 (x) 65,380.00 → shares outstanding is found on the income statement of the last fiscal year = $1,556,044.00 (in thousands).
Example 2
Calculate long-term debt.
We will simplify this process to long-term debt and capitalized leases on the company’s balance sheet and average the last 3 years’ worth of data:
| Fiscal year is January-December. All values USD Thousands. | |
|---|---|
| Long-Term Debt | |
| 2018 | $37,753.00 |
| 2019 | $18,229.00 |
| 2020 | $305,676.00 |
| Latest 3-year average | $120,552.67 |
To calculate the cost of equity in WACC, we will use the CAPM (capital asset pricing model).
However, please note that while there are other methods of valuation and modeling such as the Gordon Model, we are refraining from such complexities and keeping our model simple using the principle of Occam’s Razor.
CAPM (Capital Asset Pricing Model)
Developed by William F. Sharpe, Jack Treynor, John Lintner, and Jan Mossin.
- Exceptional tool for making decisions in portfolio investments.
William F. Sharpe is a professor of Finance (Emeritus) at UCLA
- Developed Sharpe Ratio for investment performance analysis
- Received 1990 Nobel Prize in Economics
(Risk Free Rate of Return + Beta of Asset) x (Expected Return of Market – Risk Free Rate of Return)
We use the CAPM to calculate the Cost of Equity
\(\textbf{Cost of Equity}\)
\[\begin{eqnarray}
&=& \frac{E(R_i)-R_f}{\beta_i}=E(R_m)-R_f\\
\\
&=& E(R_i)=R_f+\beta_i(E(R_m)-R_f)\\
\\
E(R_i) &=& \text{expected return of capital asset}\\
R_f &=& \href{https://fred.stlouisfed.org/series/DGS10/}{\text{risk free rate of return}}\\
\beta_i &=& \href{https://finance.yahoo.com/quote/IMAX/key-statistics?p=IMAX}{\text{beta of the asset (sensitivity)}}\\
E(R_m) &=& \href{https://finance.yahoo.com/quote/SPY/performance/}{\text{expected return of market}}
\end{eqnarray}\]
We can get the risk-free rate of return by taking the average of the 10-year Treasury Bond yields; an excellent resource for this endeavor is the St. Louis Federal Reserve. Select a 10-year date range, and download the report into Excel
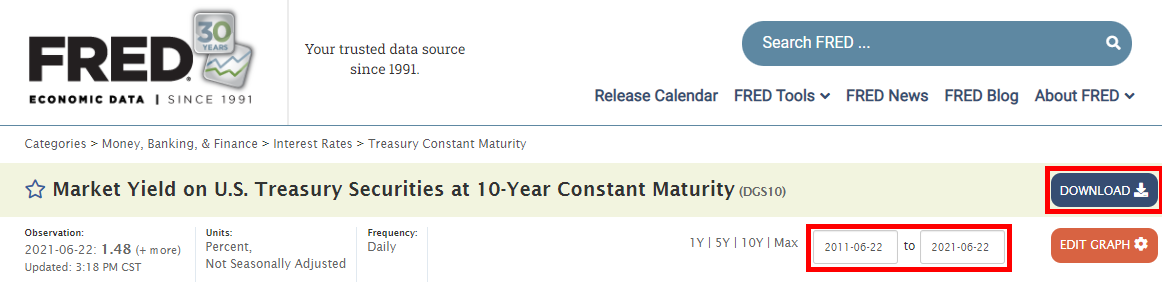
The average rate for this date range is 1.48%.
The beta of the asset can be found on Yahoo Finance
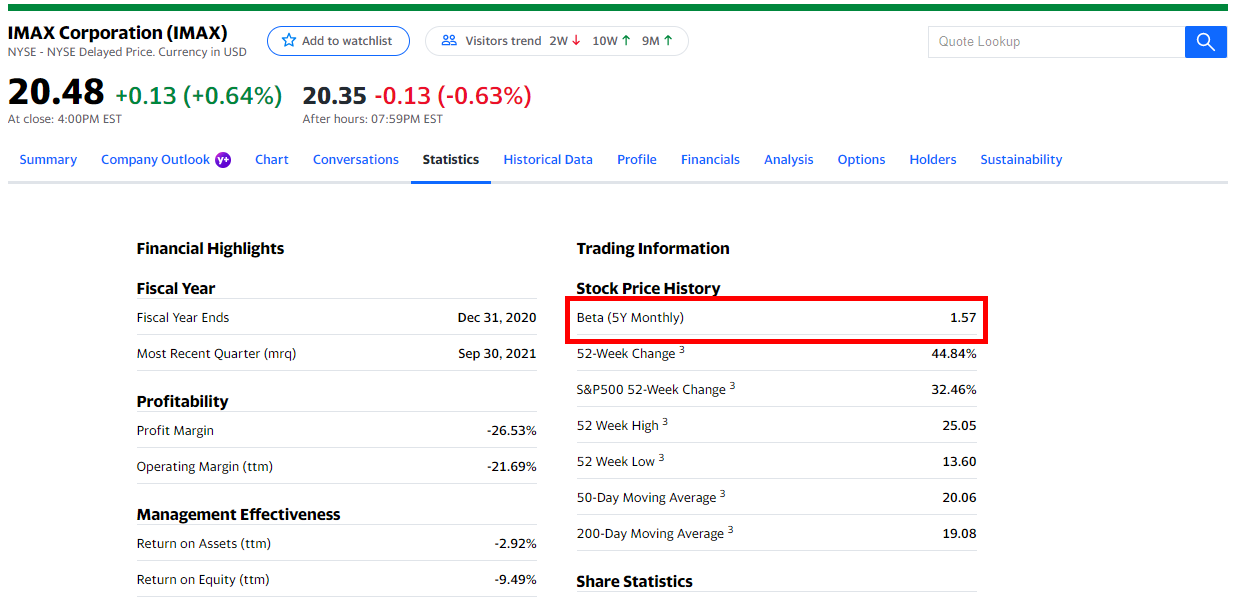
\[\begin{eqnarray} & &\beta_i &=& \text{beta of asset (sensitivity) = 1.57} \end{eqnarray}\]
The expected return of the market \(E(R_m)\) can be measured by looking at the average of the S&P 500 via Yahoo Finance as follows:
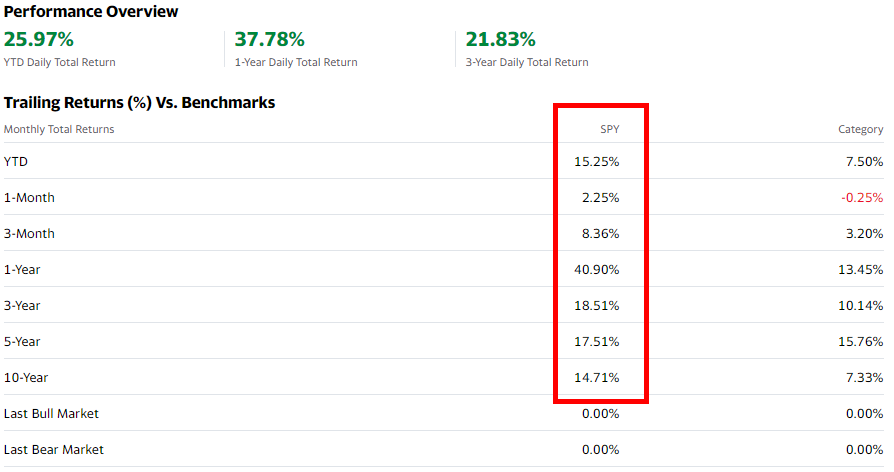
\[\begin{eqnarray} & & E(R_m) &=& \text{Average = 16.78} \end{eqnarray}\]
Example 3
Calculate the cost of debt.
\[\begin{eqnarray} \text{Cost of Debt} &=& \frac{$7,010}{$120,552.67}=0.06\\ \\ \text{Weight of Equity} &=& \frac{E}{E+D} = \frac{$1,267,079.43}{($1,267,079.43 + $26,113.33)}\\ \\ \text{Weight of Debt} &=& \frac{D}{E+D} = \frac{$26,113.33}{($1,267,079.43 + $26,113.33)}\\ \\ \text{Tax Rate} &=& \frac{\text{income tax expense}}{\text{income before tax}} \end{eqnarray}\]
| A | B | C | D | E | F | G | H | I | J | K | L | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Formula | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | Average Tax Rate | Formula | |
| 2 | Income Before Tax | 63,810.00 | 57,351.00 | 87,078.00 | 57,853.00 | 30,011.00 | 43,605.00 | 75,336.00 | -129,124.00 | 35,740.00 | <– =AVERAGE(C2:J2) | |
| 3 | Income Tax Expense | 16,629.00 | 14,466.00 | 20,052.00 | 16,212.00 | 16,790.00 | 9,518.00 | 16,768.00 | 26,504.00 | 17,117.38 | <– =AVERAGE(C3:J3) | |
| 4 | 5 Year Tax Rate | –> =C3/C2 | 26% | 25% | 23% | 28% | 56% | 22% | 22% | -21% | 32% | <– =AVERAGE(C4:G4) |
| 5 | Latest 2 Year Tax Rate | 0.866% | <– =AVERAGE(I4:J4) |
| A | B | C | |
|---|---|---|---|
| 1 | EQUITY | in thousands | Formula |
| 2 | Shares Outstanding | 59,237.00 | <– =ProForma!I47 |
| 3 | Share price | 21.39 | <– 21.39 |
| 4 | Equity value (“market cap”) | 1267079.43 | <– =B3*B2 |
| 5 | |||
| 6 | DEBT | 120552.67 | <– =ProForma!K116 |
| 7 | |||
| 8 | Cost of Equity (based on CAPM) | 16.62 | <– =B11+(B10*B22) |
| 9 | Risk-Free Rate of Return + Beta of Asset * (Expected Return of the Market - Risk-Free Rate of Return) | ||
| 10 | Beta | 0.99 | <– 0.99 |
| 11 | 10 year Treasury Rate | 0.02 | <– =‘10 year Treasury Rate’!B2622*0.01 |
| 12 | Expected Market Return (as of 11/10/2021)) | ||
| 13 | S&P500 Rate of Return | SPY | <– SPY |
| 14 | YTD | 15.25 | <– 15.25 |
| 15 | 1-Month | 2.25 | <– 2.25 |
| 16 | 3-Month | 8.36 | <– 8.36 |
| 17 | 1-Year | 40.9 | <– 40.9 |
| 18 | 3-Year | 18.51 | <– 18.51 |
| 19 | 5-Year | 17.51 | <– 17.51 |
| 20 | 10-Year | 14.71 | <– 14.71 |
| 21 | Average | 16.78 | <– =AVERAGE(B14:B20) |
| 22 | Market Premium | 16.76 | <– =B21-B11 |
| 23 | |||
| 24 | Cost of Debt | 0.06 | <– =B25/B26 |
| 25 | Interest Expense | 7,010.00 | <– =ProForma!I23 |
| 26 | Latest 3 Year Average Debt | 120552.67 | <– =B6 |
| 27 | |||
| 28 | Weight of Equity (E/(E+D)) | 0.913123466 | <– =B4/(B4+B6) |
| 29 | Weight of Debt (D/(E+D)) | 0.086876534 | <– =B6/(B4+B6) |
| 30 | |||
| 31 | Tax Rate | 0.008658066 | <– =‘Tax Rate’!K5 |
| 32 | |||
| 33 | WACC | 15.18 | <– =(B28*B8)+(B29*B24)*(1-B31) |