Neural Networks and Machine Learning in R
Leonid Shpaner
Instructions:
In this project, you will:
- Examine what common architectures are and activation functions for neural networks
- Examine how to optimize the parameters in a neural network
- Make predictions using neural networks in R
- Practice Deep Learning using R
- Apply ideas for cross-validation for neural network model development and validation
- Tune parameters in a neural network using a grid search
- Use the package Lime in R to recognize which variables are driving the recommendations your neural network is making
Part One - Projecting Data for Neural Networks
In this part of the project, you will project data for neural networks using the file ElectionData.csv, which contains the fraction of votes by county earned by President Trump and Secretary Clinton in the 2016 US Presidential election, sorted by county FIPS code (FIPS stands for Federal Information Processing System, and is a geographic identifier). The data file also includes several variables that may be useful to predict these fractions. Use the data to develop a neural network model for either individual.
This part of the project requires some work in RStudio, located on the project page in Canvas. Use that space, along with the provided script and data file, to perform the work, then use this document to answer questions on what you discover.
- How well did your model predict the election results? Before discussing the model’s predictive ability, it is necessary to dispense with a comprehensive analysis whereby the features of the dataset are examined in the following manner.
-
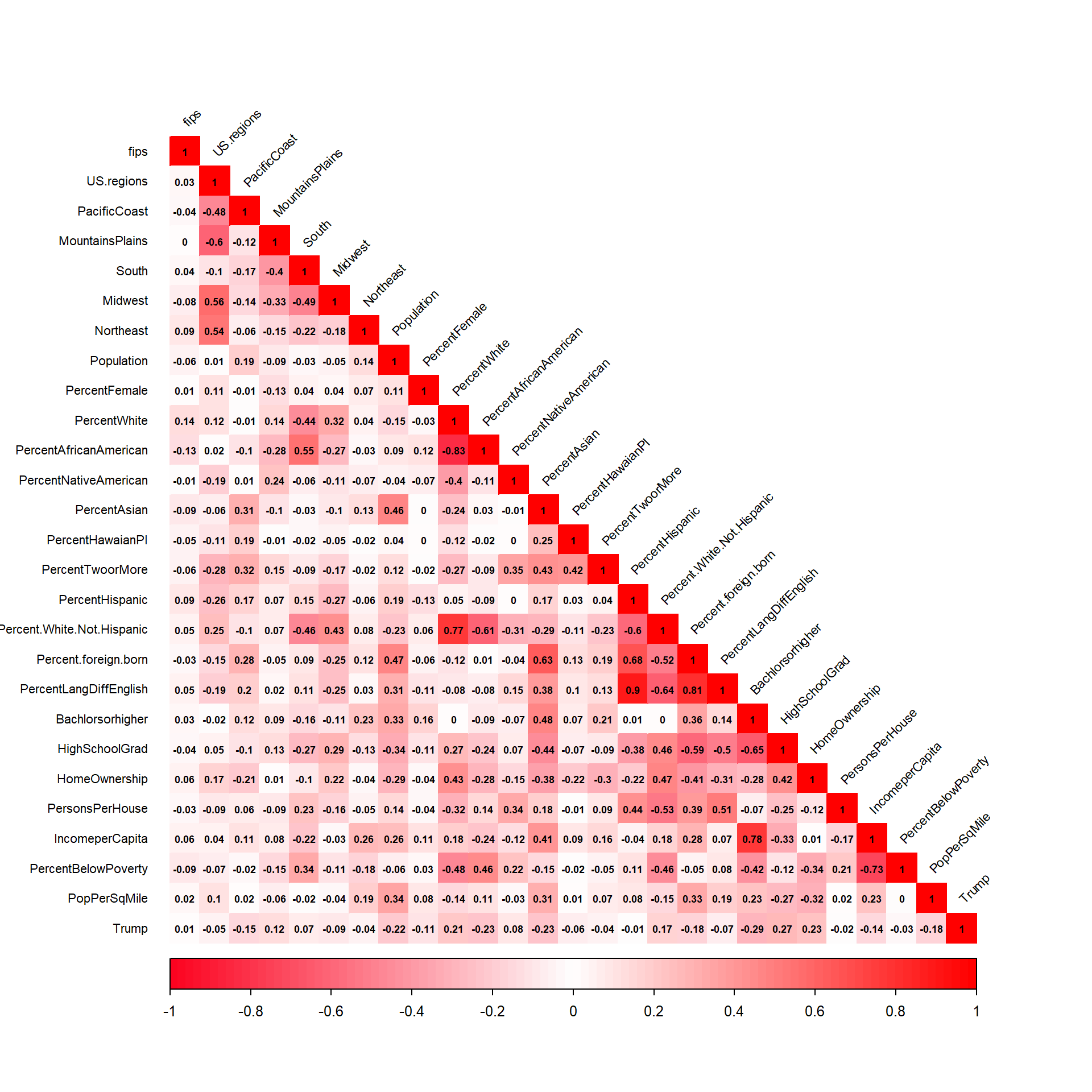
There are five highly correlated predictors above a threshold of r = 0.75 which are omitted from the model -
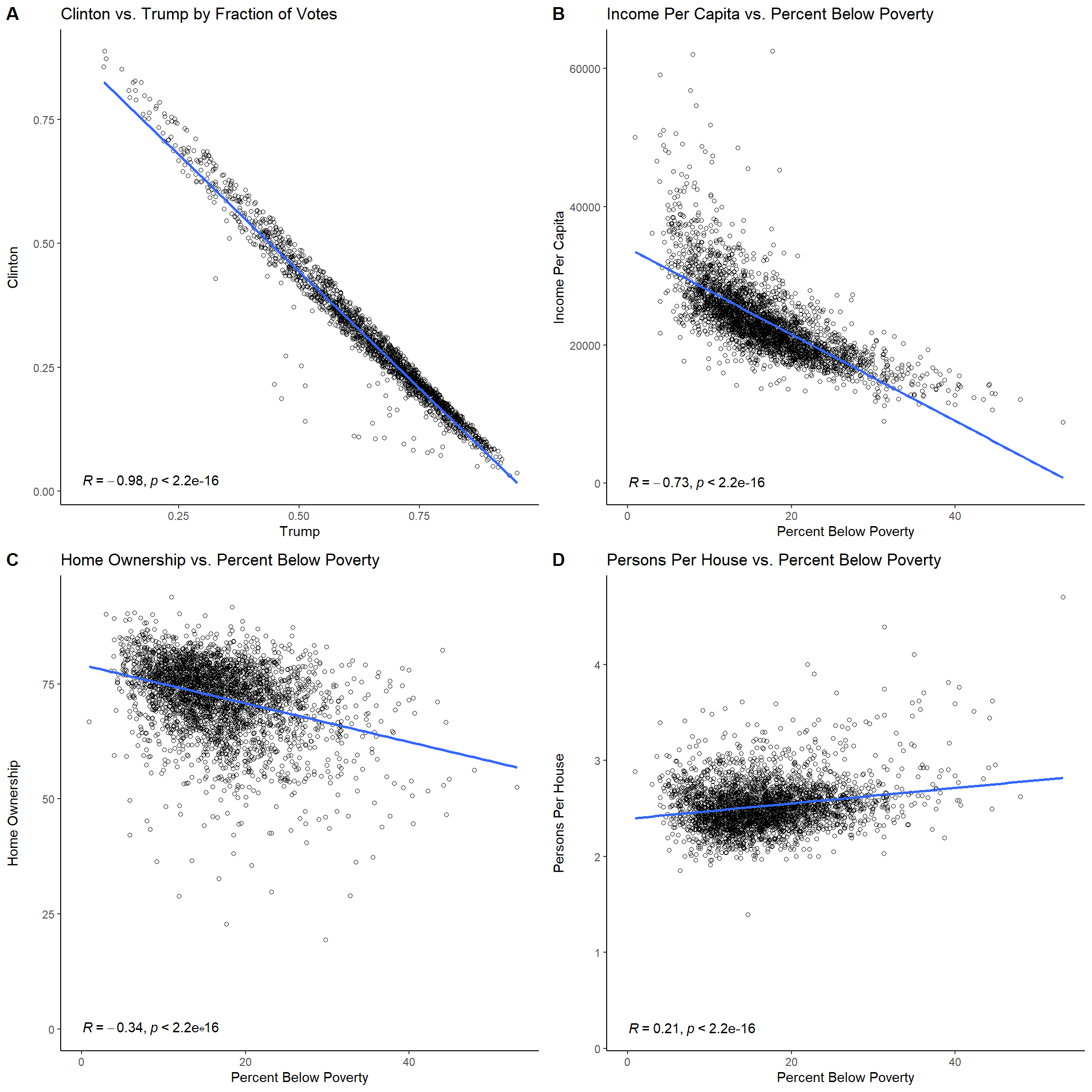
Percent.White.Not.Hispanic,Percent.foreign.born,PercentLangDiffEnglish,PercentWhite, andBachlorsorhigher. - Correlation - various economic indicators may shed light on election results. These important variable relationships are examined in the ensuing scatter plot diagrams. Plot A demonstrates that there exists a strong negative correlation (r=-0.98) between Clinton’s fraction of Votes to that of Trump’s. In Plot B, as income per capita decreases, the percent below poverty increases, so there exists a strong negative relationship (r=-0.73) between the two. Plot C shows that there is a weak (almost moderate) relationship (r=-0.34) between home ownership and percent below poverty; so, as the percent below poverty increases, home ownership begins to decrease. Lastly, persons per house shares a low correlation (r=0.21) with percent below poverty, so it is difficult to compare the two.
- The data undergoes a 70:30 train-test-split, with 70% allocated to the training set and 30% allocated to the test set.
- Prior to calling on the neural network, a generalized linear model is fitted with the training data. The following output is obtained. All features are statistically significant at an \(\alpha\) = 0.05 significance level. The mean absolute error between true and fitted values was 0.1349895 fraction of votes, so it was a fairly small error, thereby rendering the model predictions sound and proper.
Training Dimensions: 2186 27 Testing Dimensions: 957 27 Training Dimensions Percentage: 0.7 Testing Dimensions Percentage: 0.3
Call: glm(formula = Trump ~ ., data = trainingdata) Deviance Residuals: Min 1Q Median 3Q Max -9.992e-16 -3.331e-16 -1.110e-16 2.220e-16 1.166e-15 Coefficients: (2 not defined because of singularities) Estimate Std. Error t value Pr(>|t|) (Intercept) 1.112e-17 3.416e-16 3.300e-02 0.974031 fips 1.419e-21 5.556e-22 2.555e+00 0.010698 * US.regions -1.938e-16 3.539e-17 -5.477e+00 4.83e-08 *** PacificCoast -4.894e-16 1.230e-16 -3.980e+00 7.11e-05 *** MountainsPlains -5.678e-16 8.248e-17 -6.885e+00 7.57e-12 *** South -5.426e-16 5.116e-17 -1.061e+01 < 2e-16 *** Midwest NA NA NA NA Northeast NA NA NA NA Population 5.198e-23 4.696e-23 1.107e+00 0.268464 PercentFemale 1.303e-17 3.783e-18 3.444e+00 0.000583 *** PercentAfricanAmerican 1.064e-17 8.595e-19 1.238e+01 < 2e-16 *** PercentNativeAmerican 3.026e-19 1.416e-18 2.140e-01 0.830823 PercentAsian 7.091e-18 4.264e-18 1.663e+00 0.096505 . PercentHawaianPI 4.762e-18 8.261e-18 5.760e-01 0.564363 PercentTwoorMore -5.311e-18 7.205e-18 -7.370e-01 0.461098 PercentHispanic -4.935e-19 8.324e-19 -5.930e-01 0.553334 HighSchoolGrad -1.252e-17 1.774e-18 -7.054e+00 2.32e-12 *** HomeOwnership -3.491e-18 1.367e-18 -2.554e+00 0.010711 * PersonsPerHouse -3.482e-17 4.271e-17 -8.150e-01 0.415082 IncomeperCapita -1.327e-21 3.025e-21 -4.380e-01 0.661080 PercentBelowPoverty -6.857e-18 2.609e-18 -2.629e+00 0.008636 ** PopPerSqMile 1.119e-20 8.475e-21 1.320e+00 0.187033 output_train 1.000e+00 5.303e-17 1.886e+16 < 2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 (Dispersion parameter for gaussian family taken to be 1.43169e-31) Null deviance: 6.6136e+01 on 2185 degrees of freedom Residual deviance: 3.0996e-28 on 2165 degrees of freedom AIC: -149026 Number of Fisher Scoring iterations: 1
- Do you think your model will generalize well to new data? Why or why not?
- What could you do to improve the model?
- In the space below, describe your neural network structure (i.e., how many hidden layers were in the network?). How many nodes are in each hidden layer? Which activation function did you use? Which independent variables did you include? The neural network structure includes 2 hidden layers with 5 and 3 nodes, respectively:
The model should generalize well to new data because the mean absolute error on the out-of-sample (test) data is 0.1285449 (in close proximity to that of the training MAE (0.1362437)). There is a negligible difference between the two of 0.007698762.
Apart from eliminating the highly correlated predictors, various additional feature reduction techniques like PCA (Principal Component Analysis) can be applied. Furthermore, the number of hidden layers and nodes can be changed and the model hyperparameters tuned.
nn_train <- neuralnet(f_train, data=trainingdata, hidden=c(5,3), linear.output=T)
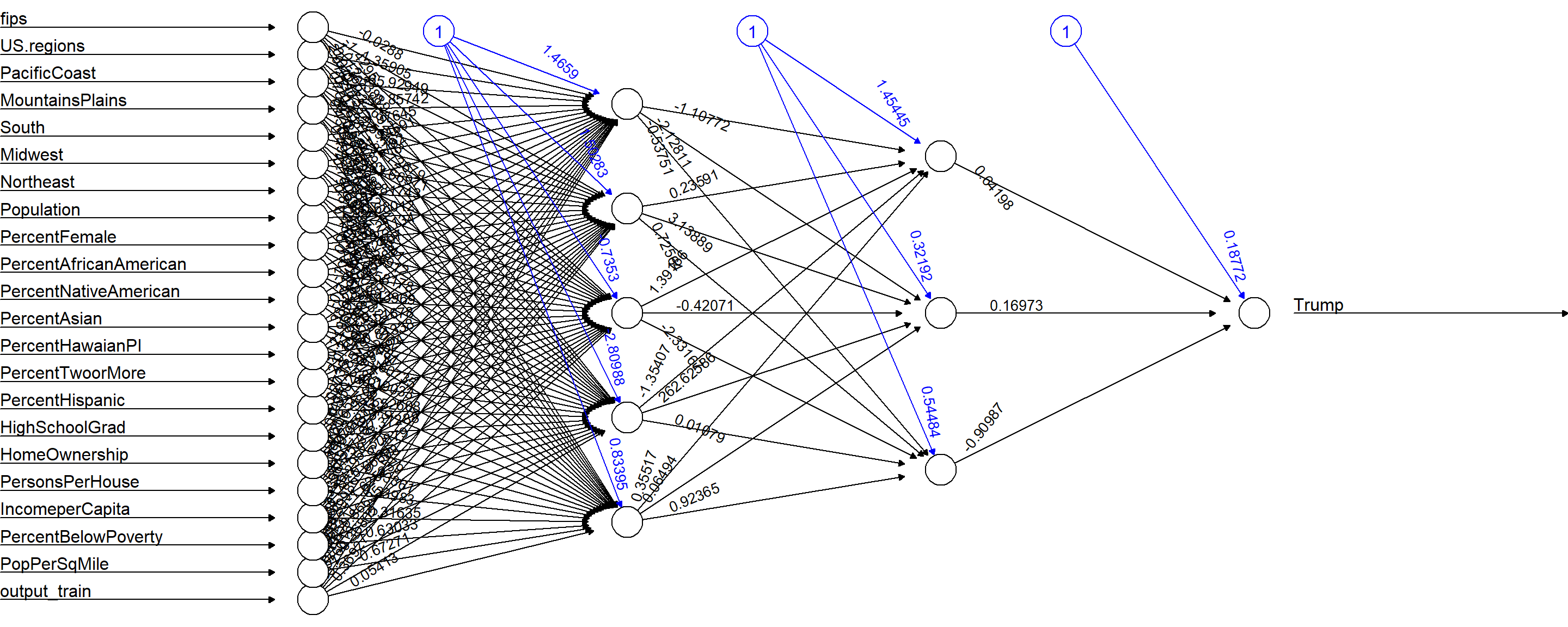 No activation (act.fct) was applied to the model, since
No activation (act.fct) was applied to the model, since linear.output was set to TRUE.
As corroborated in the prior answers, all independent variables were used, except for the five
highly correlated predictors that were identified via the correlation matrix.
Part Two
In this part of the course project, you will use H2O and LIME for neural network predictions on a data set predicting the sale prices of houses. This part of the project requires some work in RStudio, located on the project page in Canvas. Use that space, along with the provided script and data file, to perform the work, then use this document to record your accuracy measures.
Additional information:
Many attributes in this dataset are categorical. For example, ASSESSMENT_NBHD (assessment neighborhood) will need to be converted to numerical data from a neighborhood name. Consider carefully how you might do this. There are also a lot of variables, and it will be easy to overfit your model. To this end, in the deeplearning() function in H2O, there is a setting called L2. Investigate this setting and see if you find it valuable. There is also a function h2o.varimp_plot() that will create a histogram of the relative importance of all the inputs to your model. That might help you decide how to select variables for inclusion in your final model.
When constructing your model, also consider the following:
- Explore the data set with scatter plots and compute the correlation matrix.
- Split the entire dataset into a training and test set, and both should be converted into H2O data frames. The test set should contain a random sample of roughly 30% of the entire data.
- Select several data points from the training data set to analyze with LIME later on.
- Fit the neural network using
h2o.deeplearning()- Decide which independent variables to include.
- Decide how many hidden layers to include in the network.
- Decide how many nodes will be in each hidden layer.
- Decide which activation function to use (for reference, h2o supports the following: “Tanh”, “TanhWithDropout”, “Rectifier”, “RectifierWithDropout”, “Maxout”, “MaxoutWithDropout” ).
- Specify whether or not to use an adaptive learning rate (argument: adaptive_rate).
- L1 regularization can result in many weights being set to 0, add stability, and improve generalization. Set the l1 argument (larger values correspond to more regularization).
- L2 regularization can result in many weights being set to small values, add stability, and improve generalization. Set the l2 argument (larger values correspond to more regularization). Note: if the L1 coefficient is higher than the L2 coefficient, the algorithm will favor L1 regularization and vice versa.
- Specify how many epochs the training algorithm should run for.
- Set the random seed argument (seed) to guarantee the same results each time you run the training algorithm.
- Decide which independent variables to include.
- Plot the training and validation loss vs. the training epochs.
- Use the
summary()function to examine the fit model.
- Use the data points selected earlier to compute and analyze the neural network’s predictions using the
lime()function from the lime package.- Visualize the results of this analysis.
- Visualize the results of this analysis.
- In this course project document, analyze the model and summarize your findings. How well does your model predict house price? Do you think it will generalize well to new data? Which variables ended up being most important? What could be done to improve the model?
- How well did your model predict the house prices?
-
Estimate The Deep Neural Network
The figure below shows the relationship between mean absolute error and number of epochs for both the training and validation sets, respectively. Generally, as the number of epochs increase, the MAE decreases, but there is a wider gap between the training and validation sets. The neural network is tuned with theTanhactivation function over 1000 epochs, four hidden layers and four nodes, respectively, anl1rate of 0.0001, andl2rate of 0.01. Moreover, theadaptive_rate,variable_importances, andreproduciblehyperparameters are set toTRUE. Cross-validation is carried out over 3 folds.
- Additional Exploratory Data Analysis (EDA)
-
Correlation Matrix
The following correlation matrix is compiled from the top 20 features and does not show any between-predictor relationships above the r=0.75 threshold.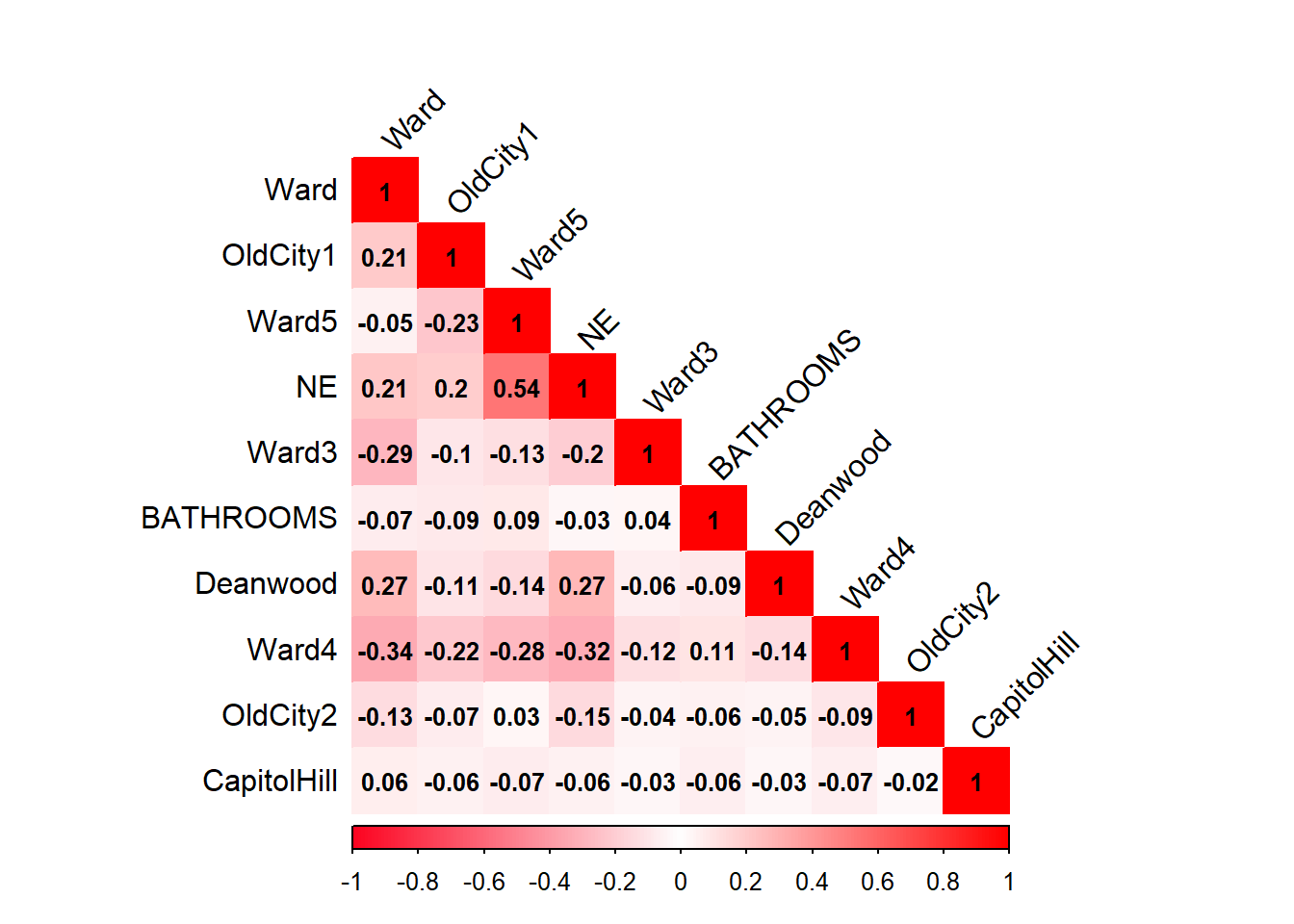
- Re-estimate the Deep Neural Network
- LIME Analysis
First and foremost, it is important to discuss data exploration. Typically, modeling commences after the data has been sufficiently explored. However, in this exercise, the data is modeled and explored in an alternating fashion. The dataset consists of 108 variables which are subsequently reduced to 90.
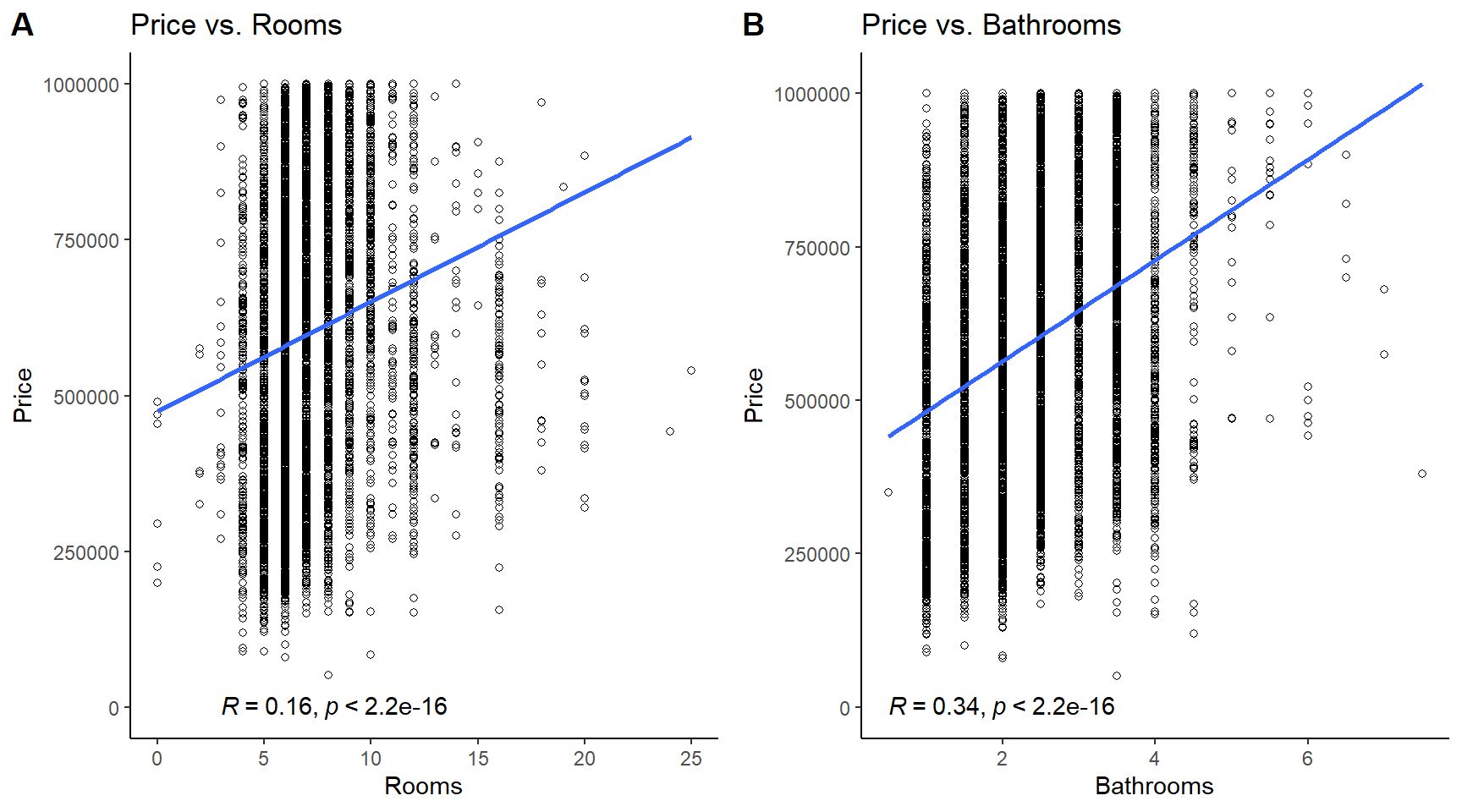
The 20 most important variables will be taken into consideration, but scatter plots on the full dataset (not training) are created only for columns with quantitative and continuous values. Price vs. rooms and price vs. bathrooms both exhibit low correlations (r=0.16, and r=-0.21, respectively). There is not much to conclude here.
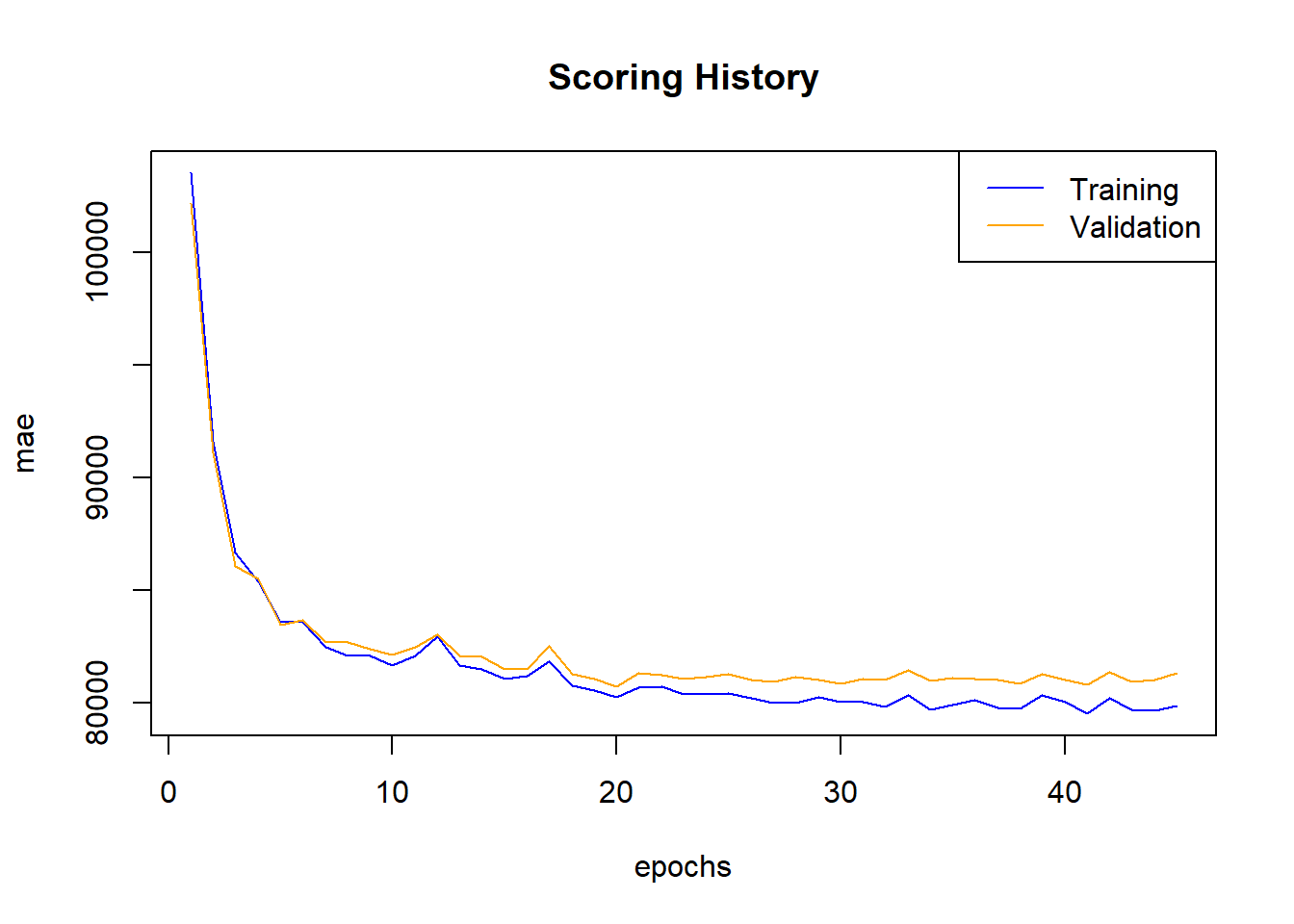
The model is re-trained with the top 20 features over the same hyperparameters as the original model. There exists a narrower gap between the training and validation MAE scores over roughly the first twenty epochs. However, the gap progressively widens.
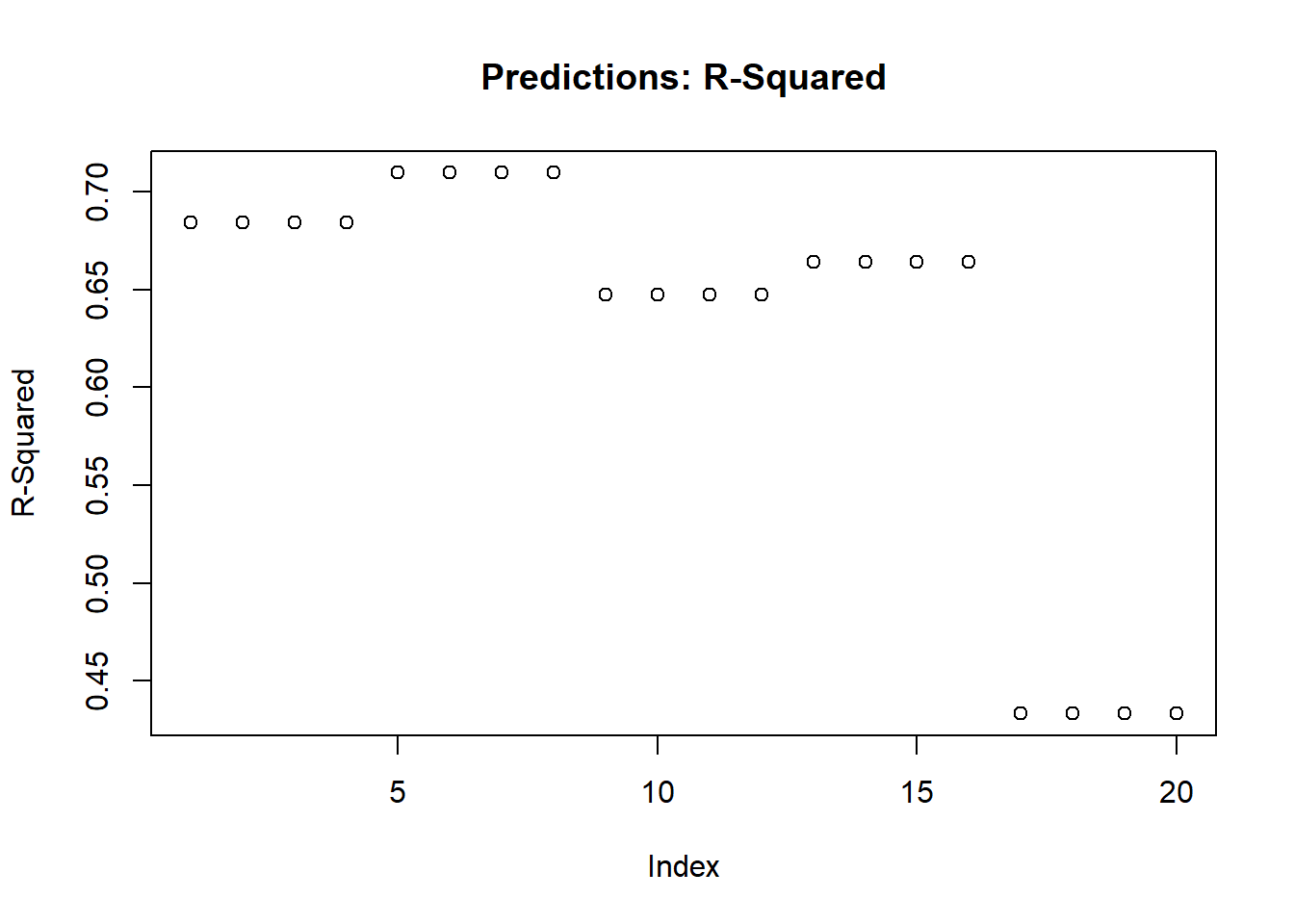
Using only the top 20 input features and the LIME package library, a substantial amount of variation is explained by the data according to the \(R^2\) values - the highest of which is 0.71, but starts off as 0.68, and then increases, but decreases in a step-wise pattern to .65, until it gradually drops off and reaches 0.43, a moderate amount of variation.
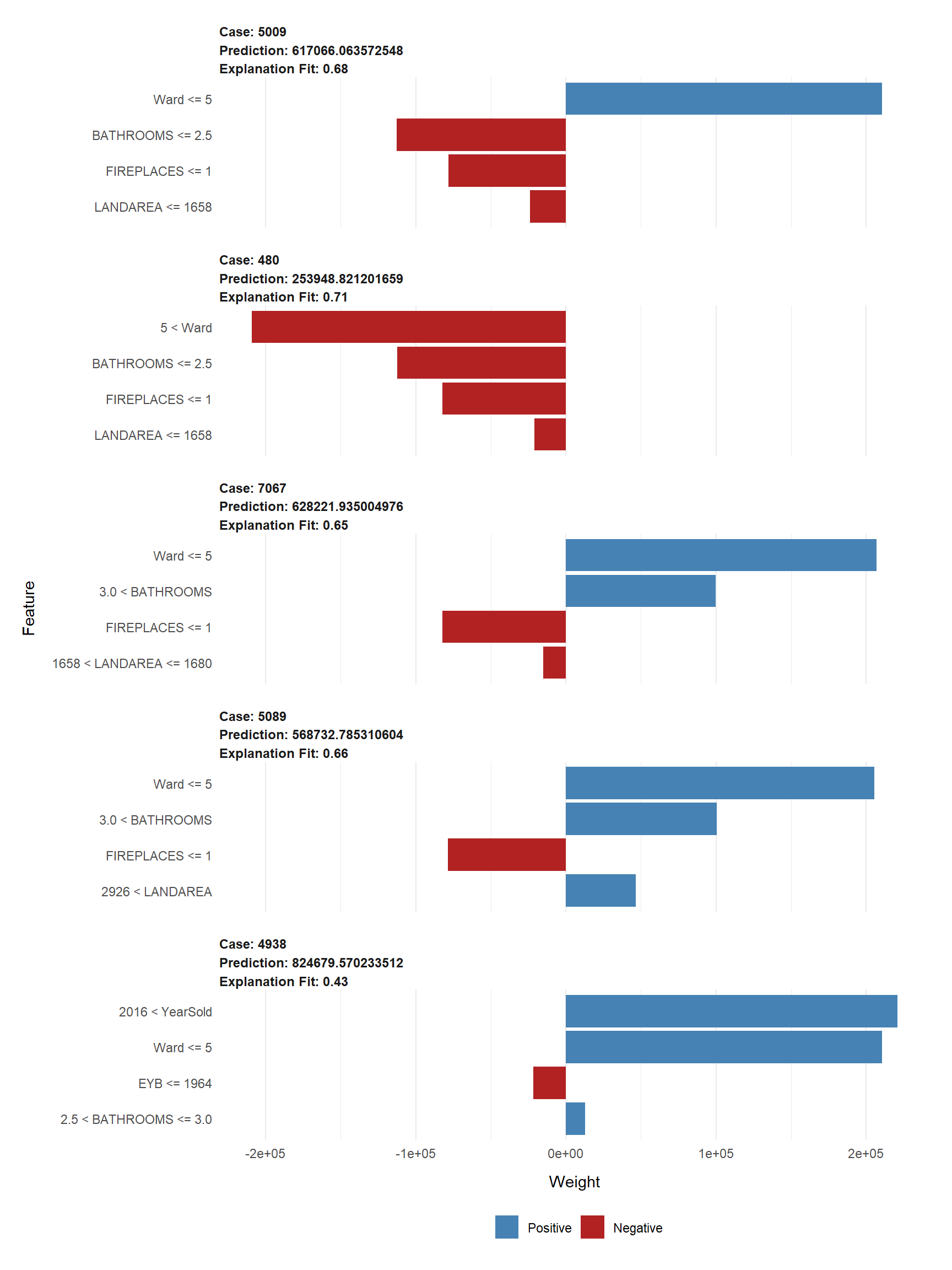
## case model_r2 model_intercept model_prediction feature prediction ## ------ ---------- ----------------- ------------------ ------------ ------------ ## 5009 0.6843 517791 513531 Ward 617066 ## 5009 0.6843 517791 513531 BATHROOMS 617066 ## 5009 0.6843 517791 513531 FIREPLACES 617066 ## 5009 0.6843 517791 513531 LANDAREA 617066 ## 480 0.7096 729583 304552 Ward 253949 ## 480 0.7096 729583 304552 BATHROOMS 253949 ## 480 0.7096 729583 304552 FIREPLACES 253949 ## 480 0.7096 729583 304552 LANDAREA 253949 ## 7067 0.6472 430790 640012 Ward 628222 ## 7067 0.6472 430790 640012 BATHROOMS 628222 ## 7067 0.6472 430790 640012 FIREPLACES 628222 ## 7067 0.6472 430790 640012 LANDAREA 628222 ## 5089 0.664 418250 692433 Ward 568733 ## 5089 0.664 418250 692433 BATHROOMS 568733 ## 5089 0.664 418250 692433 FIREPLACES 568733 ## 5089 0.664 418250 692433 LANDAREA 568733 ## 4938 0.4334 401948 824680 Ward 824680 ## 4938 0.4334 401948 824680 EYB 824680 ## 4938 0.4334 401948 824680 BATHROOMS 824680 ## 4938 0.4334 401948 824680 YearSold 824680
Moreover, the mean price prediction of $578,529.80 differs by only $19,528.26 from the actual mean housing price of $598,058.10. That is an almost negligible difference of approximately 3%, so the model predicted well.
The ensuing plots show how five random features explain the model’s fit with a mean of 63%.
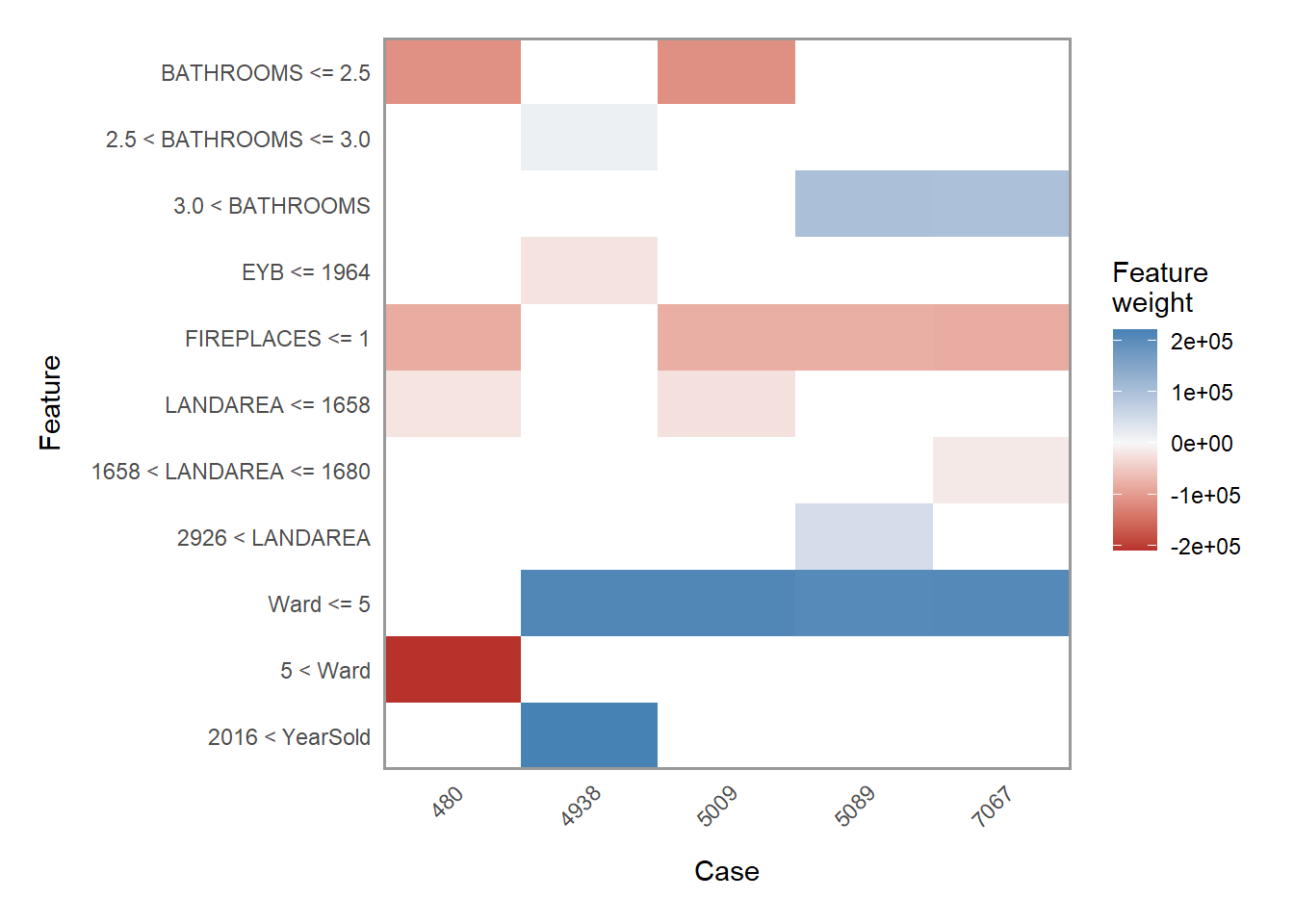
- Do you think your model will generalize well to new data? Why or why not?
- Which variables ended up being the most important and why do you think this is so?
- What could you do to improve the model?
- In the space below, describe your neural network structure (i.e., which independent variables did you use?). How many hidden layers were in the network? How many nodes were in each hidden layer? Which activation function did you use? Did you use an adaptive learning rate? How many epochs did the training algorithm run for?
The 613.31 difference in the mean absolute error between the train (80,587.15) and validation (81,200.46) sets is negligible. However, at each time step of the epoch progression, that difference becomes wider, and thus, will not generalize well to new data unless the epochs are limited.
Using the var_imp() function call, the following variables ended up being most important:
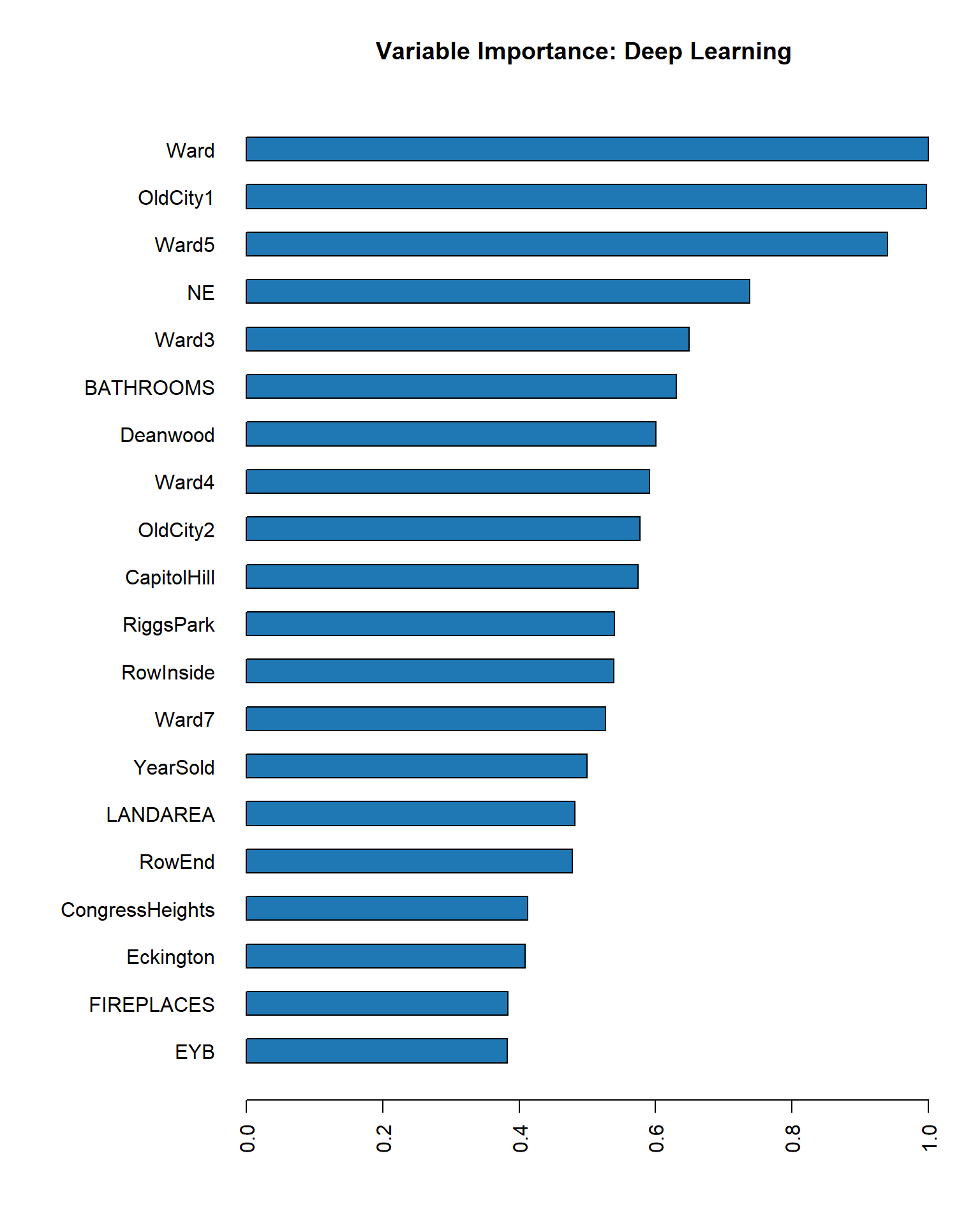
## Variable Importances: ## variable relative_importance scaled_importance percentage ## 1 Ward 1.000000 1.000000 0.162422 ## 2 EYB 0.584610 0.584610 0.094954 ## 3 OldCity1 0.581093 0.581093 0.094382 ## 4 BATHROOMS 0.456646 0.456646 0.074170 ## 5 NE 0.403440 0.403440 0.065528 ## 6 Ward4 0.322812 0.322812 0.052432 ## 7 CapitolHill 0.273834 0.273834 0.044477 ## 8 Ward7 0.268182 0.268182 0.043559 ## 9 LANDAREA 0.250221 0.250221 0.040641 ## 10 OldCity2 0.237900 0.237900 0.038640 ## 11 CongressHeights 0.221452 0.221452 0.035969 ## 12 RowInside 0.216636 0.216636 0.035187 ## 13 Deanwood 0.206530 0.206530 0.033545 ## 14 RowEnd 0.198102 0.198102 0.032176 ## 15 FIREPLACES 0.194298 0.194298 0.031558 ## 16 Ward3 0.185223 0.185223 0.030084 ## 17 YearSold 0.178580 0.178580 0.029005 ## 18 RiggsPark 0.165993 0.165993 0.026961 ## 19 Eckington 0.108953 0.108953 0.017696 ## 20 Ward5 0.102287 0.102287 0.016614
Number of bathrooms and bedrooms, among other features are important predictors in real estate data because they drive price.
Additional preprocessing like one-hot encoding other columns with many classes could prove beneficial. Understanding the dataset better would also lead to better preprocessing, which would ultimately lead to better model creation. Additional iterations with cross-validation over 5 folds and a more robust hyperparameter tuning mechanism like that of grid search could be implemented. Grid search on a CPU with 4 cores and 8 logical processors at a base speed of 2.30 GHz would not do this endeavor any justice. To this end, it may be necessary to purchase a more powerful computer with gaming GPUs.
The final (third iteration) model’s neural network structure includes all twenty of the top most important features listed in number 4. 2 hidden layers and 2 nodes were used, respectively, with an activation function of Tanh. The adaptive learning rate was passed in and set to TRUE, even though it is set to TRUE by default. The model was iterated through 1,000 epochs.