Supervised Learning Techniques in R
Leonid Shpaner
Part One
Building A Model
In this part of the project, you will focus on building a model to understand who might make a good product technician if hired using linear discriminate analysis logit and ordered logit modeling. The data set you will be using is in the file HRdata2groups.csv, contained in the RStudio instance.
-
The four performance scores in
Notice that you have a several variables that might be used as independent variables. You should pick the variables to include based on how effective they are at explaining the variability in the dependent variable as well as which variables might be available should you need to use this model to determine if a candidate is likely to make a good employee. You may assume that the verbal and mechanical scores will be available at the point where a decision about hiring is to be made. In this question, please give us the linear discriminate model you have developed.PerfScorehave been mapped into two new categories of Satisfactory and Unsatisfactory under the heading ofCollapseScore. Assume that levels 1 and 2 are unacceptable and levels 3 and 4 are acceptable. Build a linear discriminant analysis using regression with these two categories as the dependent variable. The purpose of this question is for you to examine the independent variables and conclude which one to include in the regression model. Several are not useful. Remember that when we do this, only the coefficients in the model are useful. You may use the functionlm()which has the syntaxlm(dependent variable ~ independent variable 1+ independent variable 2+…, data=frame). This function is part of the package caret: hence you will need to use the commandlibrary(caret). - Explain the variables you decided to use in the model described above and why.
-
The regression model can be used to classify each of the individuals in the dataset. As discussed in the videos, you will need to find the cutoff value for the regression value that separates the unsatisfactory performers from the satisfactory performers. Find this value and determine whether individual 5 is predicted to be satisfactory or not.
In R you can use the predict command to use the regression function with the data associated with each individual in the dataset. For example:
pred=predict(model, frame)stores the predicted values from the regression function into the variable pred when the regression model has been assigned to the variable model as in this statement:model <-lm(dependent variable ~ independent variable 1+ independent variable 2+…, data=frame).You may then find the mean value of the regression for all observations of unsatisfactory employees using the command
meanunsat=mean(pred[frame$CollapseScore==0]).The cutoff value is then computed in r as follows:
If you want to compare what your model says verses whether they were found to be satisfactory or unsatisfactory you may add the prediction to the data frame usingcutoff<-0.5(meanunsat+meansat).cbind(frame, pred). This will make the predictions part of the dataset. -
Construct a logit model using the two performance groups. Compare this model and the discriminant analysis done in step 1. To construct the logit model, use the function
lrm()in the library rms. -
Build an ordered logit model for the full four categories for performance. When you call the function
lrm()you will use the original categoriesPerScoreID. What is the probability that individual two is in each of the four performance categories? You can use the functionpredict()to do this. The form of the call ispredict(name of the model you used when you created the model, data=frame, type=”fitted.ind”).
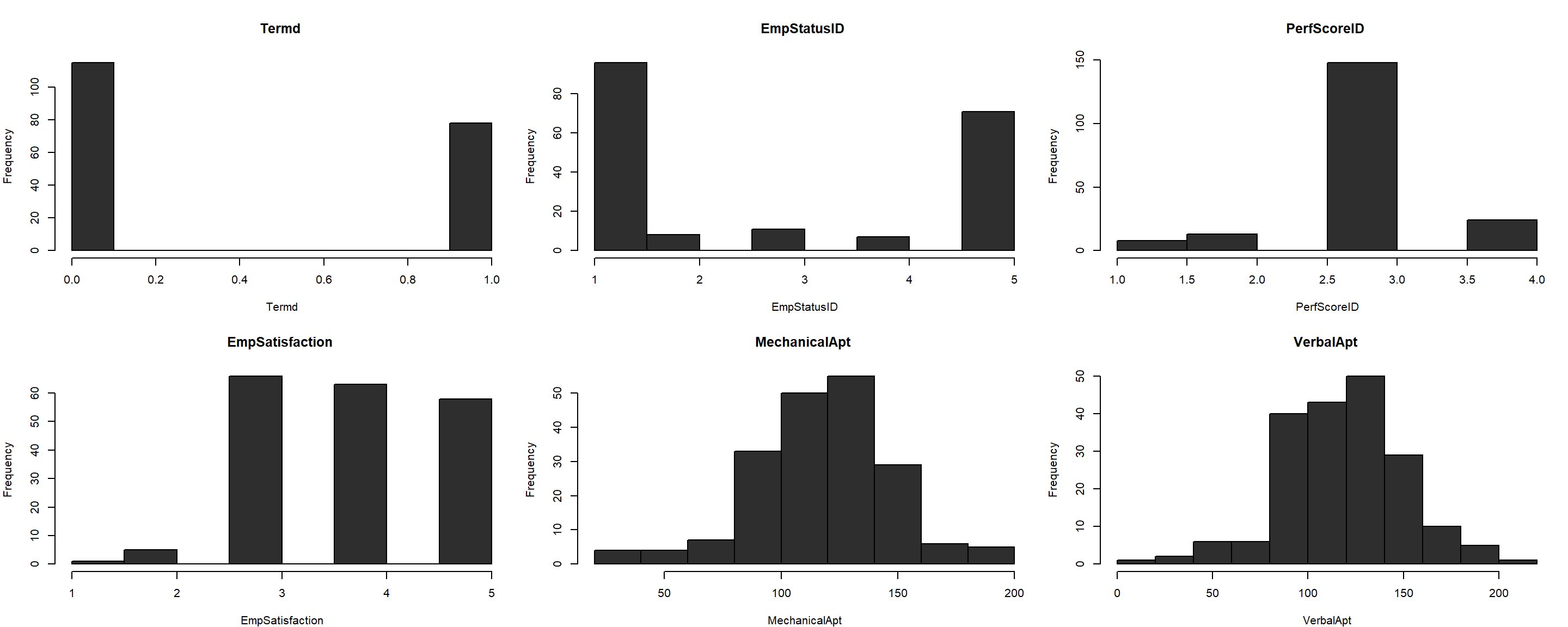
The dataset is inspected and the categorical classes of Acceptable and Unacceptable are cast to the Performance Score (PerfScoreID) in a new column named CollapseScore. However, since supervised learning models need to learn from a numerical, though, binarized target column, a new column of Score is thus created. Extraneous or otherwise not useful columns like Employee ID, CollapseScore, and Score are removed such that a numerical only dataframe is created for subsequent distribution analysis.
The histogram distributions below do not yield or uncover any near-zero-variance predictors, but it is worth noting that Termd has only two class labels. MechanicalApt and VerbalApt exhibit normality; other variables approach the same trend.
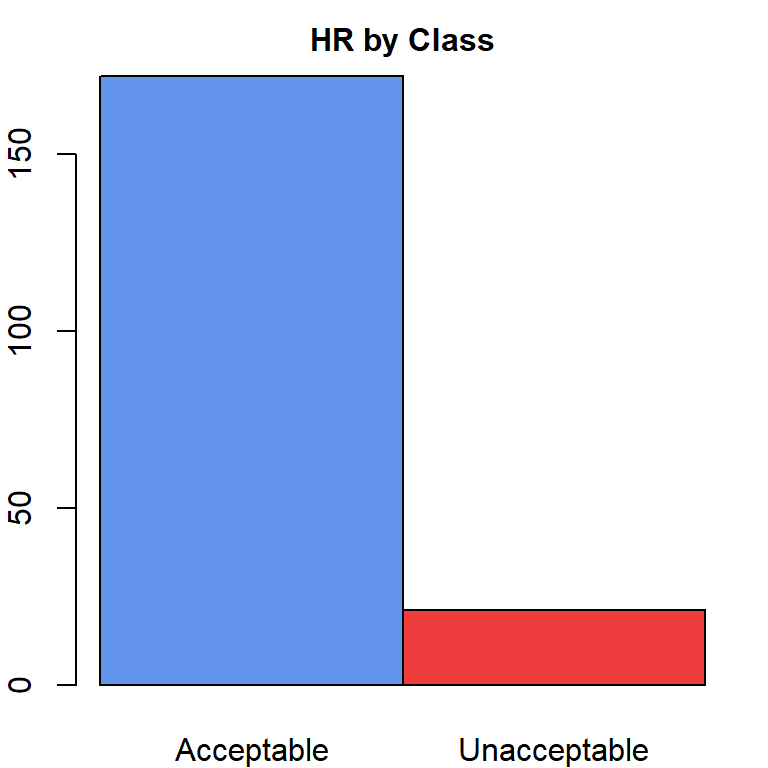
Examining the Score column separately yields an imbalanced dataset where 172 Acceptable cases outweigh the 21 Unacceptable classes. However, no solution is rendered for this outcome. The data is treated as-is.
The employee’s hiring status EmpStatusID in conjunction with the employee’s satisfaction EmpSatisfaction and average aptitude score are used in the model.
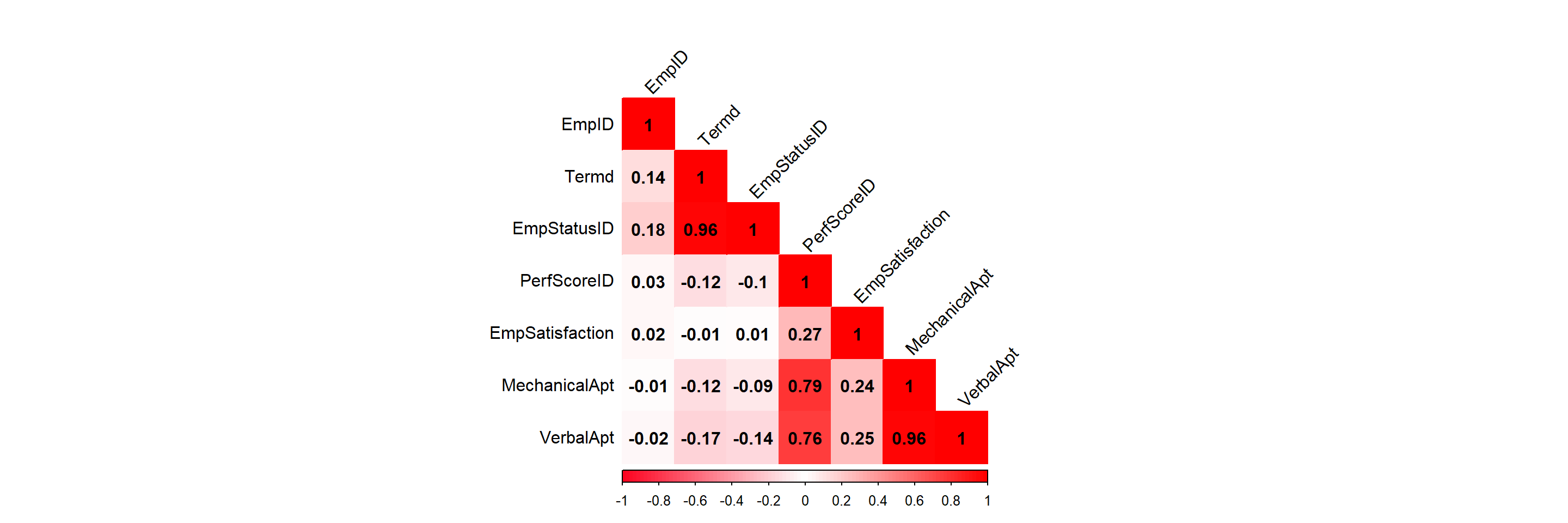
Averaging the mechanical and verbal scores row over row creates a new Aptitude column with these values. Mechanical and verbal aptitude scores are omitted because of their high between-predictor relationships. MechanicalApt vs. VerbalApt yields an r = 0.96. Once the scores are averaged and passed into one column, the problem of multicollinearity is removed. Termd is also omitted because its correlation with EmpStatusID is r = 0.96.
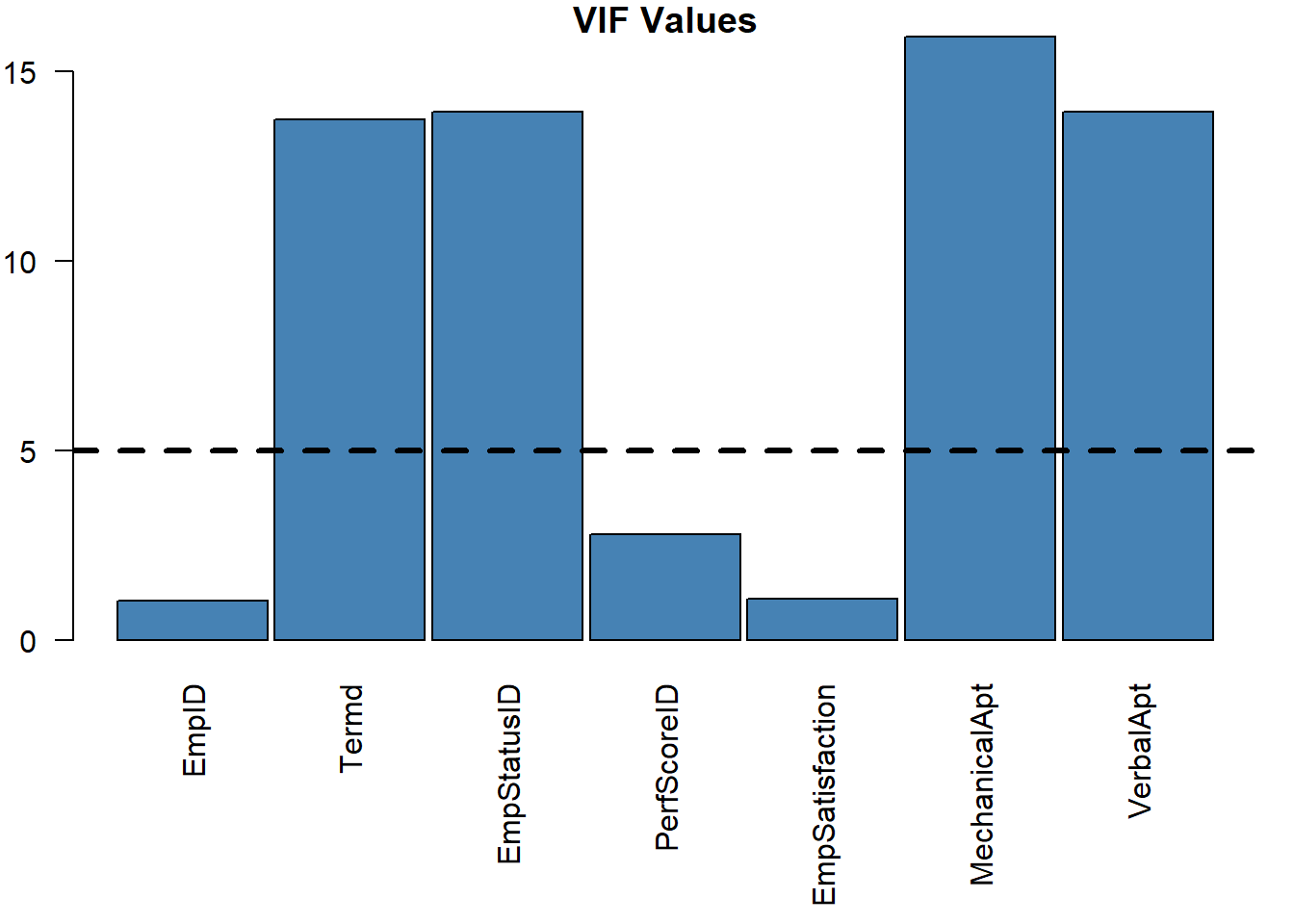
Variance Inflation Factor (VIF) scores confirm similar behavior, exhibiting high multicollinearity once a threshold of five is reached and surpassed. A linear model (lm) is used to test this behavior.
| EmpID | Termd | EmpStatusID | PerfScoreID | EmpSatisfaction | MechanicalApt | VerbalApt |
|---|---|---|---|---|---|---|
| 1.058 | 13.74 | 13.93 | 2.785 | 1.096 | 15.91 | 13.94 |
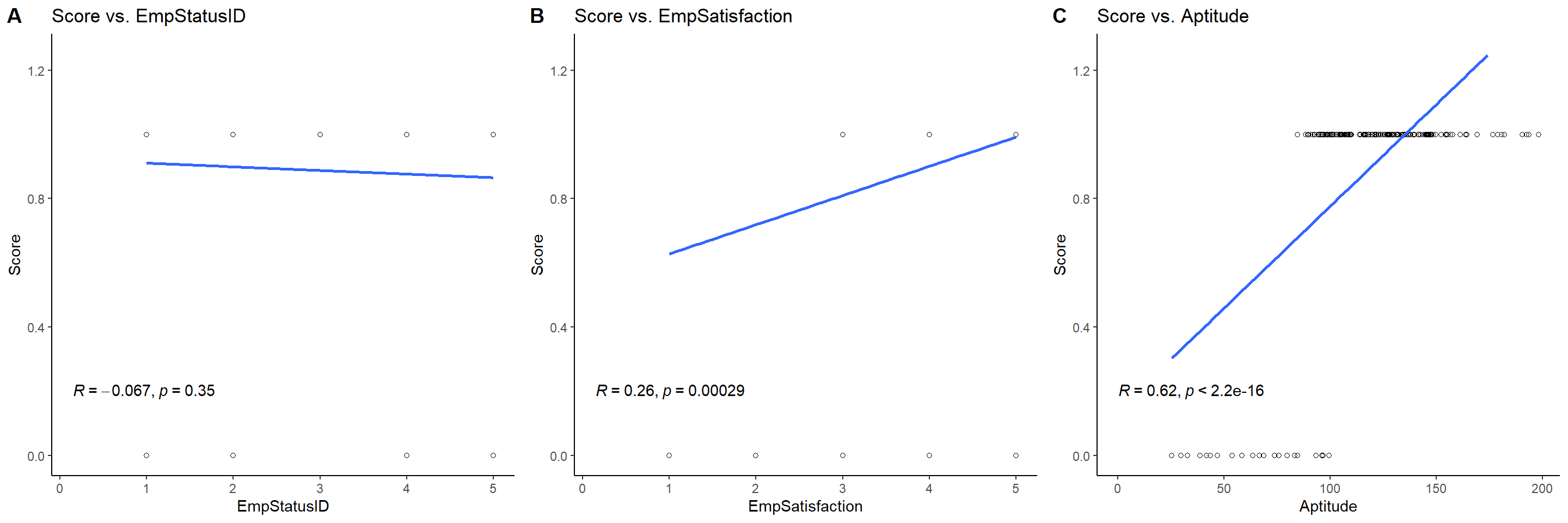
The Score vs. Aptitude scatterplot below exhibits a moderate correlation of r = 0.62. Employee satisfaction exhibits a much weaker relationship of r = 0.26, and there is almost no relationship between Score and Employee Status ID where r = -0.067.
Fitting the linear discriminant analysis model produces the following results.
Call: lda(Score ~ EmpStatusID + EmpSatisfaction + Aptitude, data = hr_data_final) Prior probabilities of groups: 0 1 0.1088083 0.8911917 Group means: EmpStatusID EmpSatisfaction Aptitude 0 3.095238 3.238095 64.41122 1 2.691860 3.970930 124.64620 Coefficients of linear discriminants: LD1 EmpStatusID 0.00271593 EmpSatisfaction 0.25572719 Aptitude 0.03966111
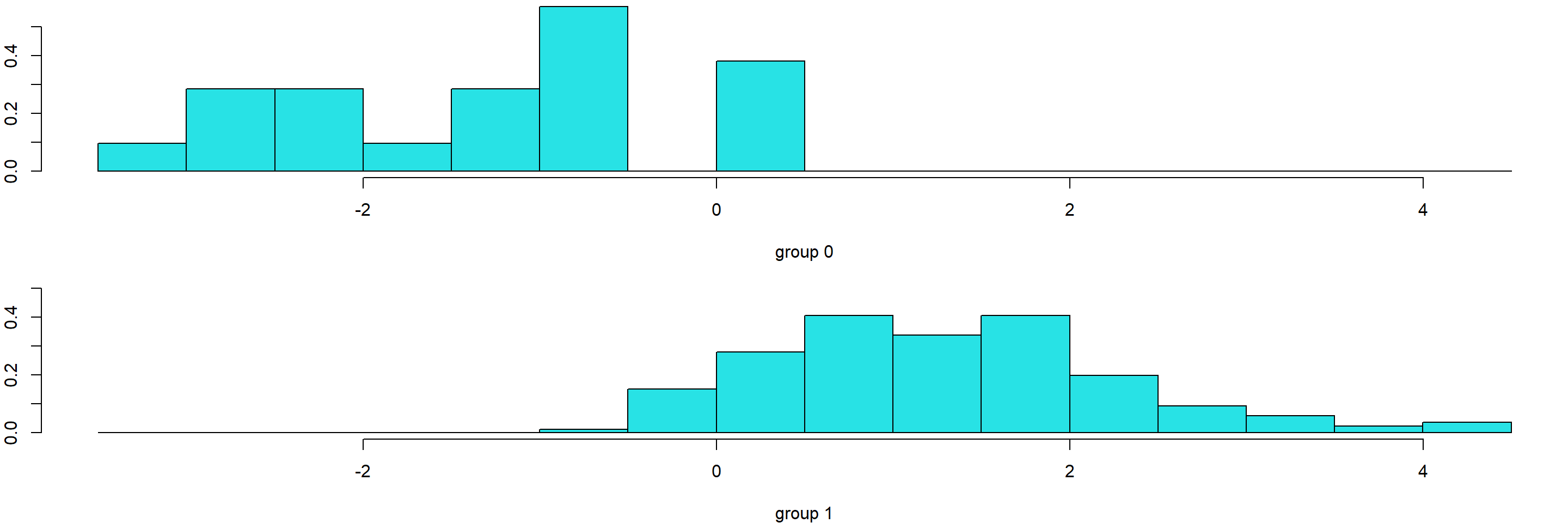
A generalized linear model is fitted accordingly, a column of predictions is appended to the dataframe, and a cutoff value is determined accordingly. Individual 5 has unacceptable/unsatisfactory performance, and the model predicts the same with a probability of 0.471, which is below the cutoff of 0.737.
|
Mean of Satisfactory Results = 0.9340495 Mean of Unsatisfactory Results = 0.5401660 Cutoff Value = 0.7371078 |
||||||
|---|---|---|---|---|---|---|
| Individual # | EmpStatusID | EmpSatisfaction | CollapseScore | Score | Aptitude | Preds |
| 1 | 1 | 5 | Acceptable | 1 | 180.9 | 1.315 |
| 2 | 1 | 3 | Acceptable | 1 | 106.7 | 0.7863 |
| 3 | 5 | 4 | Acceptable | 1 | 152.3 | 1.104 |
| 4 | 1 | 2 | Unacceptable | 0 | 46.99 | 0.3852 |
| 5 | 1 | 5 | Unacceptable | 0 | 41.87 | 0.4715 |
| 6 | 1 | 4 | Acceptable | 1 | 131.6 | 0.9764 |
Logistic Regression Model lrm(formula = Score ~ MechanicalApt + VerbalApt, data = hr_data) Model Likelihood Discrimination Rank Discrim. Ratio Test Indexes Indexes Obs 193 LR chi2 109.40 R2 0.870 C 0.991 0 21 d.f. 2 R2(2,193)0.427 Dxy 0.983 1 172 Pr(> chi2) <0.0001 R2(2,56.1)0.852 gamma 0.983 max |deriv| 3e-06 Brier 0.017 tau-a 0.192 Coef S.E. Wald Z Pr(>|Z|) Intercept -33.7121 11.5108 -2.93 0.0034 MechanicalApt 0.4697 0.1689 2.78 0.0054 VerbalApt -0.0865 0.0743 -1.16 0.2443
The linear discriminant analysis model does not use mechanical aptitude and/or verbal aptitude as standalone independent variables. The scores are averaged to create one column for Aptitude.
Logistic Regression Model lrm(formula = PerfScoreID ~ Termd + EmpStatusID + EmpSatisfaction, data = hr_data) Frequencies of Responses 1 2 3 4 8 13 148 24 Model Likelihood Discrimination Rank Discrim. Ratio Test Indexes Indexes Obs 193 LR chi2 12.13 R2 0.077 C 0.634 max |deriv| 8e-09 d.f. 3 R2(3,193)0.046 Dxy 0.268 Pr(> chi2) 0.0070 R2(3,105.5)0.083 gamma 0.298 Brier 0.086 tau-a 0.105 Coef S.E. Wald Z Pr(>|Z|) y>=2 1.0880 0.9065 1.20 0.2300 y>=3 -0.0130 0.8869 -0.01 0.9883 y>=4 -4.3212 0.9741 -4.44 <0.0001 Termd -1.2239 1.1992 -1.02 0.3075 EmpStatusID 0.1560 0.3152 0.49 0.6208 EmpSatisfaction 0.5872 0.2086 2.81 0.0049
| Individual # | PerfScoreID=1 | PerfScoreID=2 | PerfScoreID=3 | PerfScoreID=4 |
|---|---|---|---|---|
| 1 | 0.0151 | 0.0289 | 0.7297 | 0.2263 |
| 2 | 0.0472 | 0.0824 | 0.7875 | 0.0829 |
| 3 | 0.0478 | 0.0833 | 0.7870 | 0.0819 |
| 4 | 0.0818 | 0.1295 | 0.7409 | 0.0478 |
| 5 | 0.0151 | 0.0289 | 0.7297 | 0.2263 |
| 6 | 0.0268 | 0.0496 | 0.7837 | 0.1399 |
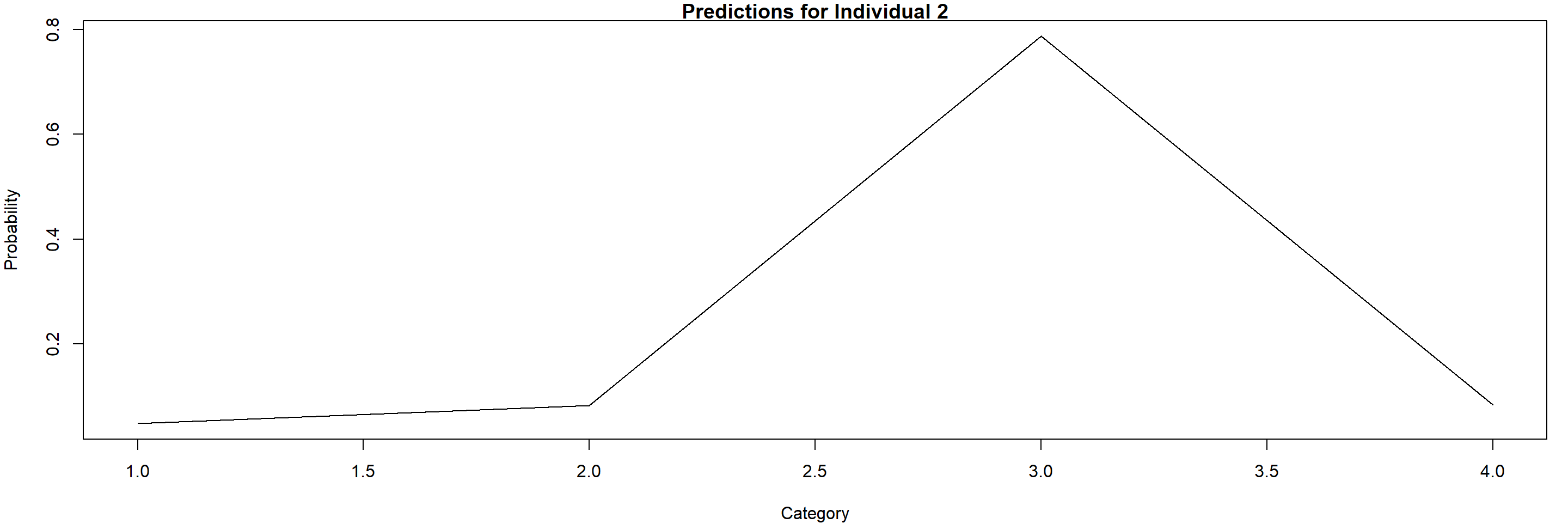
The respective probabilities that individual two will be in each of the four performance categories are 0.0472, 0.0824, 0.7875, 0.0829.
Part Two
Using Naïve Bayes to Predict a Performance Score
In this part of the project, you will use Naïve Bayes to predict a performance score. This part continues the scenario from Part One and uses the same modified version of the human resources data set available on the Kaggle website. The data set you will be using is in the file NaiveBayesHW.csv file. Over the course of this project, your task is to gain insight into who might be a “high” performer if hired.
-
Using only the mechanical aptitude score, use Naïve Bayes to predict the performance score for each employee. Professor Nozick discretized the mechanical scores into four classes. Notice only three of four classes have observations. This discretization is in the data file
NaiveBayesHW.csv. The function to create the model isnaiveBayes(). -
Using this modeling approach, what is your assessment of the probability that individual 10 will evolve into each of the four probability classes if hired? This can be done using the model created above and the
The arguments for that function are the model name, data and for type use “raw”. This question is parallel to the Practice using Naïve Bayes activity you completed in R.pred()function.
The dataset is read into this dataframe and inspected accordingly.
Naive Bayes Classifier for Discrete Predictors Call: naiveBayes.default(x = X, y = Y, laplace = laplace) A-priori probabilities: Y Class1 Class2 Class3 Class4 0.04145078 0.06735751 0.76683938 0.12435233 Conditional probabilities: MechanicalApt Y Level1 Level3 Level4 Class1 1.0000000 0.0000000 0.0000000 Class2 0.0000000 0.0000000 1.0000000 Class3 0.0000000 0.6554054 0.3445946 Class4 0.0000000 0.3333333 0.0000007 Class1 Class2 Class3 Class4 [1,] 9.999000e-05 0.1624837516 0.63743626 0.199980002 [2,] 7.617524e-05 0.0001237848 0.92362480 0.076175241 [3,] 9.999000e-05 0.1624837516 0.63743626 0.199980002 [4,] 9.773977e-01 0.0015882712 0.01808186 0.002932193 [5,] 9.773977e-01 0.0015882712 0.01808186 0.002932193 [6,] 7.617524e-05 0.0001237848 0.92362480 0.076175241 [7,] 7.617524e-05 0.0001237848 0.92362480 0.076175241 [8,] 7.617524e-05 0.0001237848 0.92362480 0.076175241 [9,] 9.999000e-05 0.1624837516 0.63743626 0.199980002 [10,] 9.999000e-05 0.1624837516 0.63743626 0.199980002 [11,] 7.617524e-05 0.0001237848 0.92362480 0.076175241 [12,] 7.617524e-05 0.0001237848 0.92362480 0.076175241 [13,] 9.999000e-05 0.1624837516 0.63743626 0.199980002 [14,] 7.617524e-05 0.0001237848 0.92362480 0.076175241 [15,] 9.999000e-05 0.1624837516 0.63743626 0.199980002 [16,] 9.999000e-05 0.1624837516 0.63743626 0.199980002 [17,] 9.999000e-05 0.1624837516 0.63743626 0.199980002 [18,] 9.999000e-05 0.1624837516 0.63743626 0.199980002 [19,] 9.999000e-05 0.1624837516 0.63743626 0.199980002 [20,] 9.999000e-05 0.1624837516 0.63743626 0.199980002
The probability that individual 10 will evolve into each of the four probability classes if hired is as follows:
| Class 1 | Class 2 | Class 3 | Class 4 | |
|---|---|---|---|---|
| Probability | 0.00009999 | 0.16248375 | 0.63743626 | 0.19998000 |
Part Three
Building Classification Trees
In this part of the project, you will build classification trees. This part continues the scenario from Parts One and Two, as it uses the same modified version of the human resources data set available on the Kaggle website. Use the HRdata4groups.csv data set to predict each individual’s performance (Performance Score ID) using classification trees. In the space below, you will explain the model you have developed and describe how well it performs.
-
In the space below, explain the model you developed. It is sufficient to use the function
ctree()in R to accomplish this in the style of the codio exercise Practice: Building a Classification Tree in R—Small Example. - In the space below, describe how well your model performs.
The dataset is read into this dataframe and inspected accordingly.
'data.frame': 193 obs. of 10 variables: $ EmpStatusID : int 1 1 5 1 1 1 1 5 5 5 ... $ PerfScoreID : int 4 3 3 1 1 4 4 3 3 3 ... $ CollapseScore : int 1 1 1 0 0 1 1 1 1 1 ... $ PayRate : num 23 16 21 20 18 16 20 24 15 22 ... $ Age : int 43 50 37 53 31 40 46 50 48 37 ... $ JobTenure : int 8 8 9 6 5 6 6 9 8 7 ... $ EngagementSurvey: num 5 5 2 1.12 1.56 3.39 4.76 3.49 3.08 3.18 ... $ EmpSatisfaction : int 5 3 4 2 5 4 4 4 4 3 ... $ MechanicalApt : num 174.6 110.6 148.6 49.1 42.2 ... $ VerbalApt : num 187.2 102.7 156.1 44.9 41.6 ...
Before modeling can commence, it is important to establish between-predictor relationships and the potential presence of multicollinearity, because this is a refined dataset from a new .csv file. The classification trees model is developed from all variables except for mechanical aptitude and verbal aptitude. Verbal aptitude exhibits a noticeably high correlation of r = 0.96 with mechanical aptitude. However, rather than omitting this one variable, both aptitude columns are replaced with a new column by the name of aptitude which has been averaged from their results.
The following variables should be omitted:
VerbalApt
VerbalApt exhibits multicollinearity, so it is averaged with MechanicalApt , just like in part one. A replacement column called Aptitude is once again created on this refined dataset.
Between-predictor relationships are once again re-examined to ensure no residual multicollinearity is detected.
Model formula: PerfScoreID ~ EmpStatusID + CollapseScore + PayRate + Age + JobTenure + EngagementSurvey + EmpSatisfaction + Aptitude Fitted party: [1] root | [2] CollapseScore <= 0 | | [3] Aptitude <= 53.89066: 1.000 (n = 8, err = 0.0) | | [4] Aptitude > 53.89066: 2.000 (n = 13, err = 0.0) | [5] CollapseScore > 0 | | [6] Aptitude <= 154.50311: 3.052 (n = 154, err = 7.6) | | [7] Aptitude > 154.50311: 3.889 (n = 18, err = 1.8) Number of inner nodes: 3 Number of terminal nodes: 4 Correct Classification of Data Point: 0.1088083null device
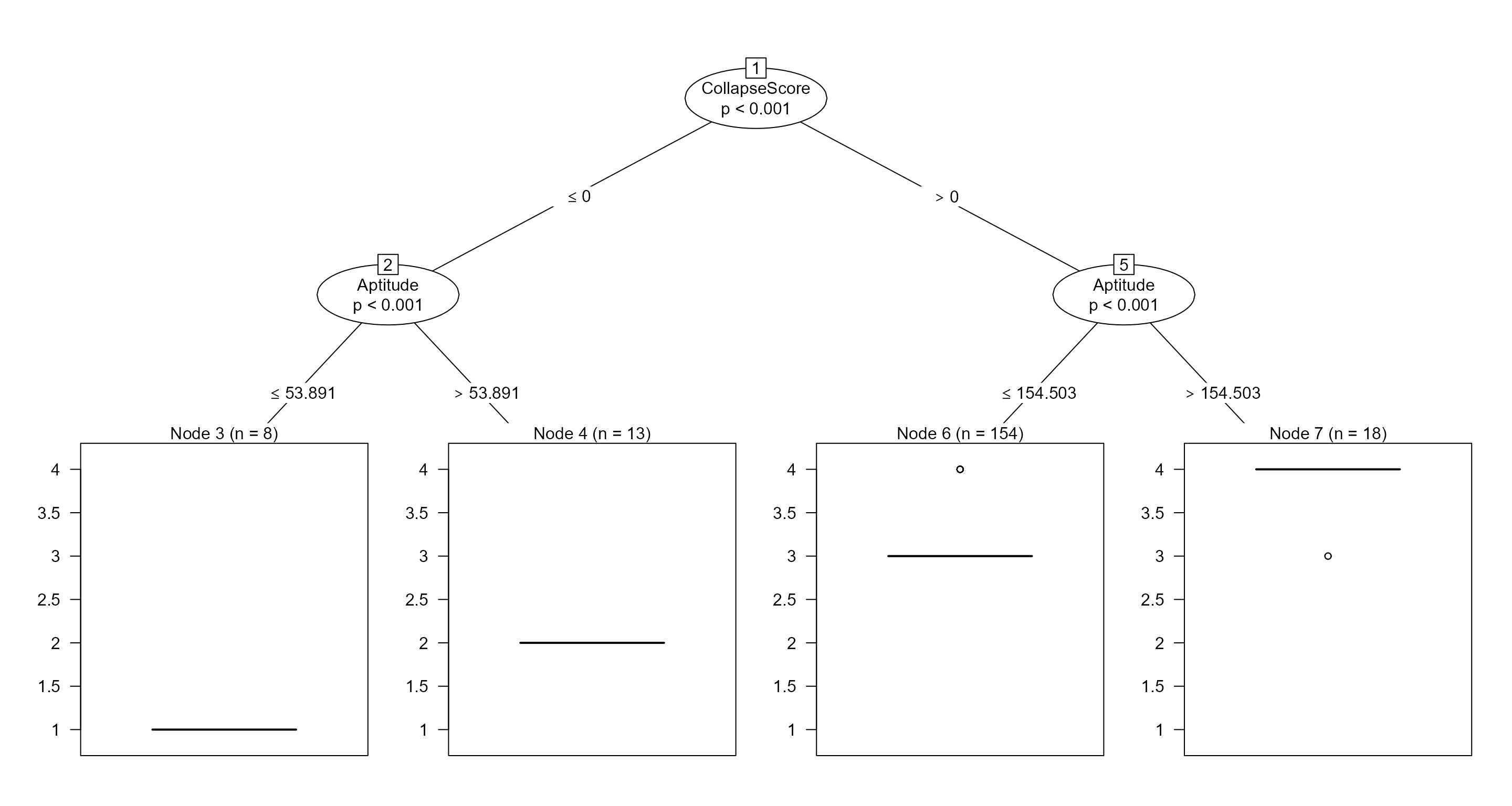
Whenever a CollapseScore is less than or equal to zero, it is classified as unacceptable or unsatisfactory performance. Thus, under this umbrella category, aptitude scores less than or equal to 53.89 (level 1) exhibit no error (third node), where n = 8. Aptitude scores greater than 53.89066 (level 2) exhibit no error, where n = 13.
Whenever a CollapseScore is greater than 0, employee performance is classified as acceptable or satisfactory. Under this umbrella category, aptitude scores less than or equal to 154.50 reach a node level of 3.052, with an error of 7.6, where n = 154 observations. Aptitude scores greater than 154.50 reach a higher node level of 3.89, where there are n = 18 observations, and a lower error rate of 1.8.
There are three inner nodes and four terminal nodes, with a correct classification of data points at approximately 11%. The performance is low, and this model warrants iterative refinement.
Part Four
Applying SVM to a Data Set
In this part of the project, you will apply SVM to a data set. The RStudio instance contains the file acquisitionacceptanceSVM.csv, which includes information about whether or not homeowners accepted a government offer to purchase their home.
-
Apply the tool SVM to the acquisition data set in the CSV file
acquisitionacceptanceSVM.csvto predict which homeowners will most likely accept the government’s offer. What variables did you choose to use in your analysis? - How good was your model at correctly predicting who would and who would not accept the offer?
- When building models, we often use part of the data to estimate the model and use the remainder for prediction. Why do we do this? It is not necessary to do this for each of the problems above. It is essential to realize that you will need to do this in practice.
The dataset is read into this dataframe and inspected accordingly.
'data.frame': 1531 obs. of 12 variables: $ Distance : num 162.75 108.26 4.55 81.28 183.21 ... $ Floodplain : int 1 1 1 1 1 1 1 1 1 1 ... $ HomeTenure : int 1 14 19 37 9 57 11 65 1 25 ... $ Education345 : int 1 0 1 1 1 0 0 0 1 1 ... $ CurMarketValue: int 650000 30000 50000 78000 127300 35000 400000 80000 360000 300000 ... $ After : int 0 0 0 0 0 0 0 0 0 0 ... $ Price100 : int 1 1 1 1 1 1 1 1 1 1 ... $ Price75 : int 0 0 0 0 0 0 0 0 0 0 ... $ Price90 : int 0 0 0 0 0 0 0 0 0 0 ... $ Price110 : int 0 0 0 0 0 0 0 0 0 0 ... $ Price125 : int 0 0 0 0 0 0 0 0 0 0 ... $ Accept : int 0 0 0 1 0 1 0 0 0 0 ...
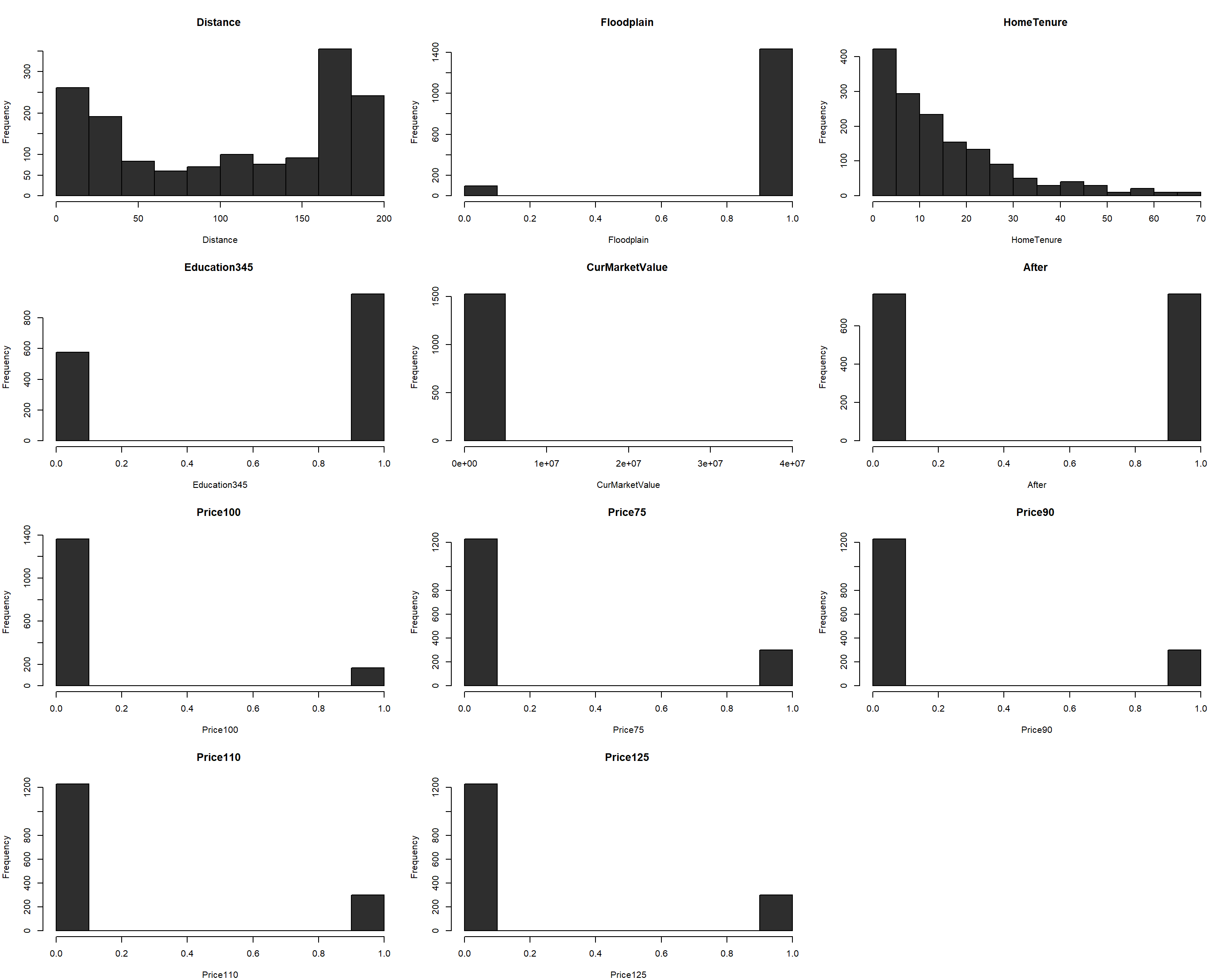Inspecting the dataframe for near zero variance predictors from a visual standpoint alone identifies current market value CurMarketValue to be a variable that exhibits such behavior. However, the nearZeroVar function from the caret library does not expose such variables. Near zero variance measures the fraction of unique values in the columns across the dataset.
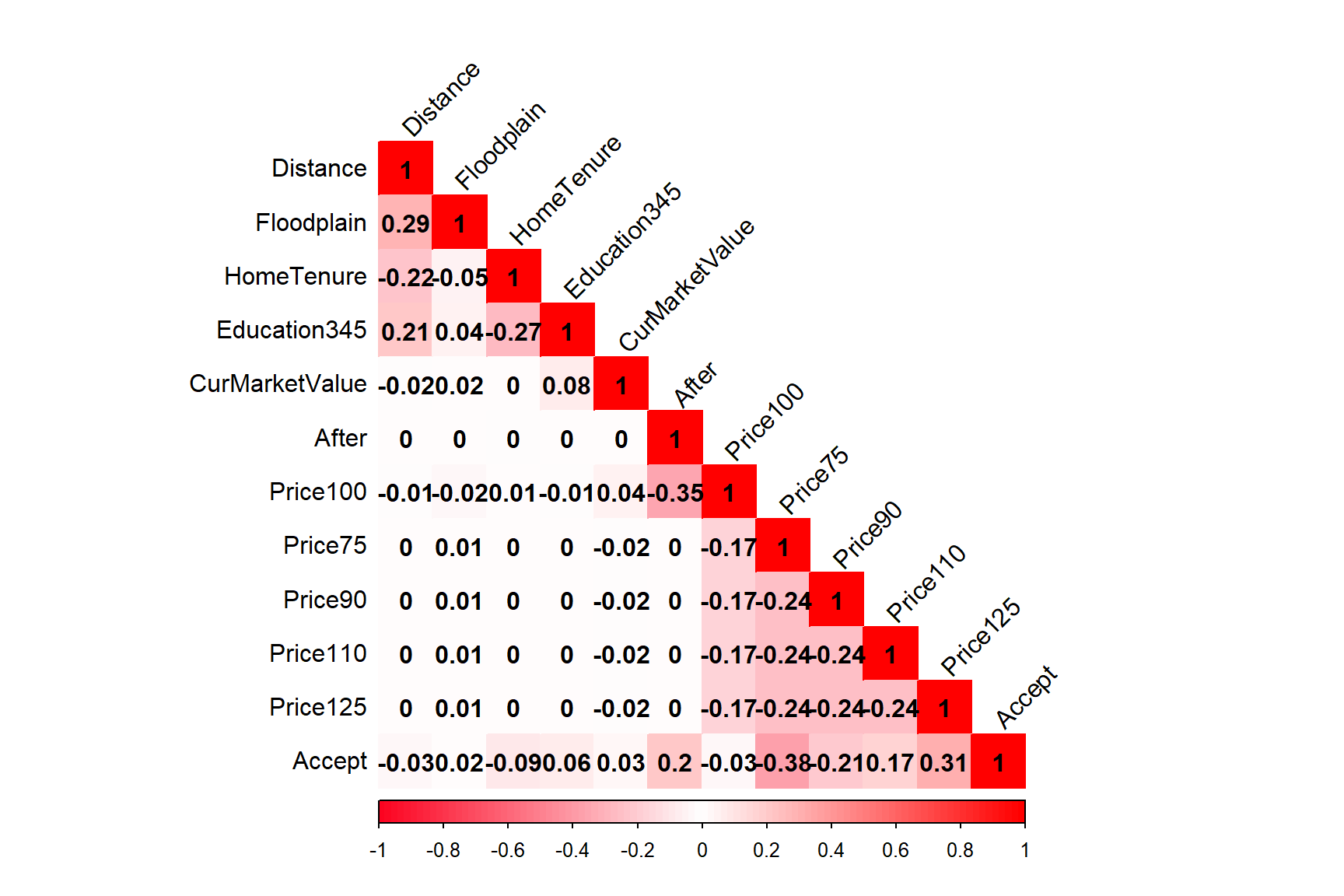
Moreover, the correlation matrix does not expose any sources of high between-predictor relationships (beyond the cutoff point of r = 0.75). This relegates the variable selection process to Principal Component Analysis (PCA), but this is a dimensionality reduction technique; there are only 12 variables and 1,531 rows of data.
Casting the target Accept variable to a factor is done to categorize the data. There are enough rows in this dataset to carry out a train-test split, and so it is done, with 70% partitioned into the training set, and the remaining 30% into the test set.
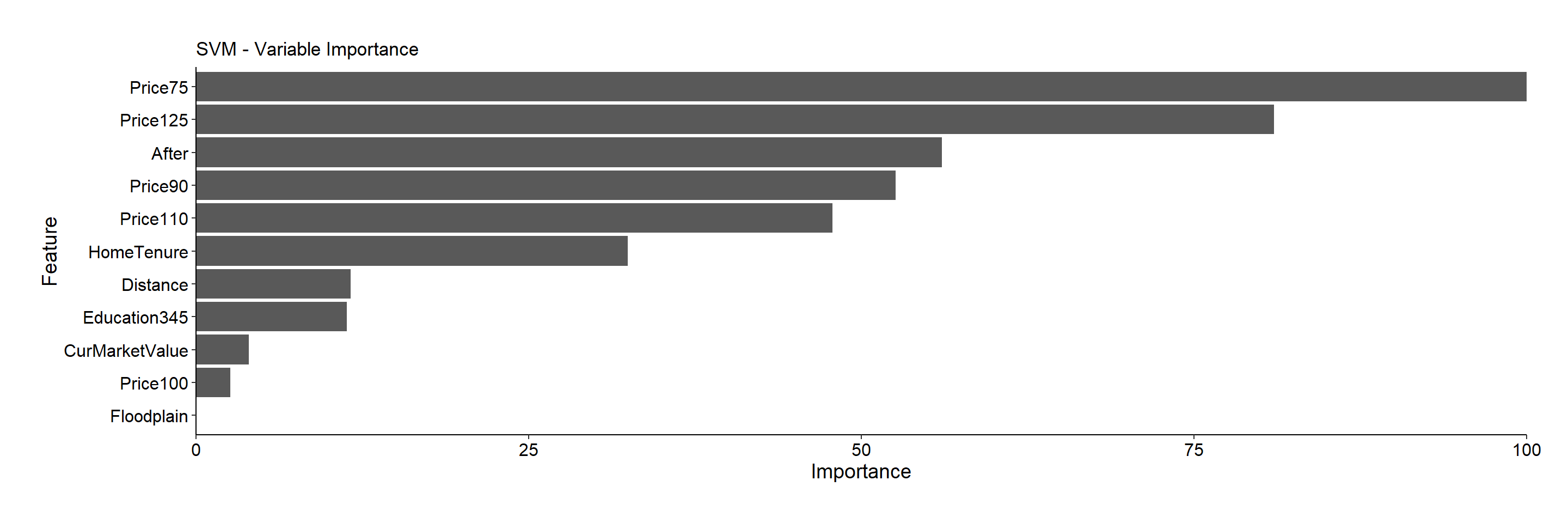
Since the e1071 package does not allow for a printout of variable importance varImpt() ) for feature selection, the caret package is used to accomplish this task, and the results are shown below. Price75 and Price125 are the top two variables surpassing a score of 80 in importance and are thus selected for the soft-margin support vector machine.
The model’s cost and kernel hyperparameters are tuned over the training data with a 10-fold cross validation sampling method. The optimal hyperparameter values are shown in table below.
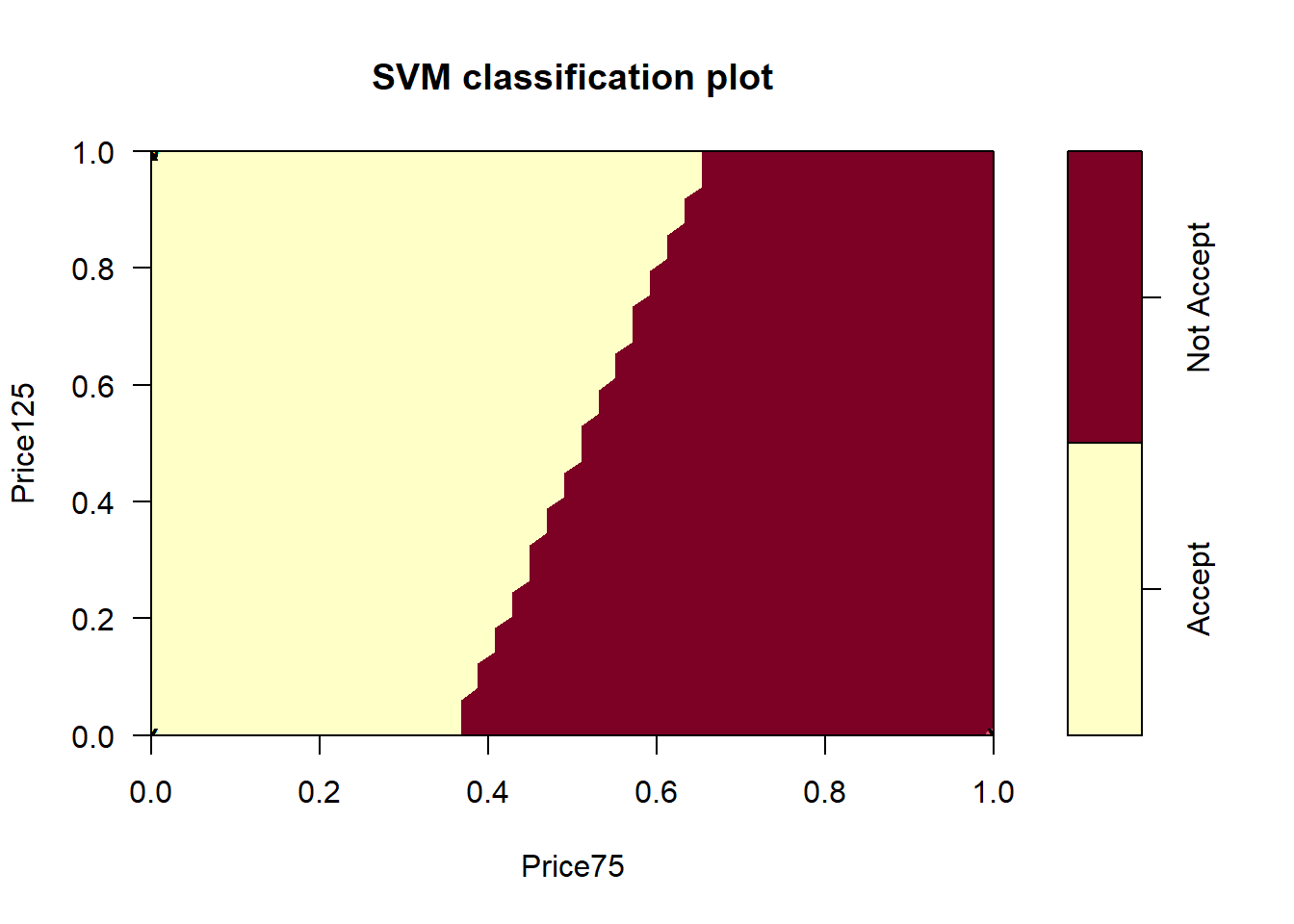
The classification results are visualized below.
| Confusion Matrix for Train Set | ||
|---|---|---|
| Accept | Not Accept | |
| Accept | 498 | 350 |
| Not Accept | 25 | 194 |
| Confusion Matrix for Test Set | ||
|---|---|---|
| Accept | Not Accept | |
| Accept | 233 | 150 |
| Not Accept | 11 | 70 |
The confusion matrix is used to obtain the first effective measure of model performance (accuracy) using the following equation.
\[\text{Accuracy} = \frac{\text{TP} + \text{TN}}{\text{TP}+\text{TN}+\text{FP}+\text{FN}}\] Precision (specificity) measures out of everyone who accepted a government offer to purchase their home, how many actually accepted? It is calculated as follows.
\[\text{Precision} = \frac{\text{TP}}{\text{TP}+\text{FP}}\]
Recall (sensitivity) measures the true positive rate (TPR), which is the number of correct predictions in the Accept class divided by the total number of Accept instances. It is calculated as follows:
\[\text{Recall} = \frac{\text{TP}}{\text{TP}+\text{FN}}\] The f1-score is the harmonic mean of precision and recall, and is calculated as follows:
\[f1 = \frac{\text{TP}}{\text{TP}+\frac{1}{2}\text{(FP+FN)}}\]
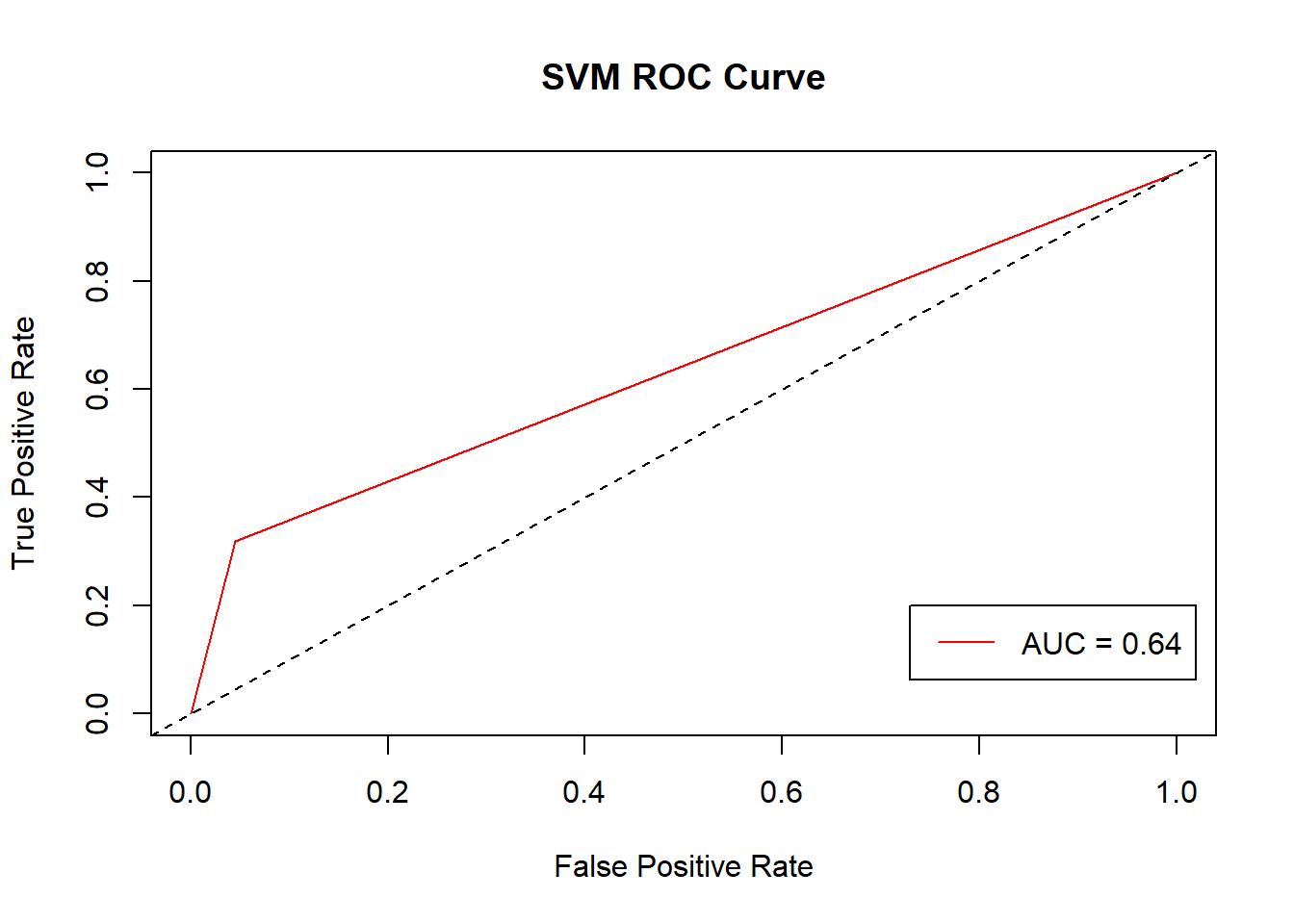
Using the test data (30% hold out), the model’s accuracy is only 15% improvement above baseline, coming out to 65%. However, the model’s ability to correctly classify the class is effectively high at 95% specificity. The ROC Curve calculates an AUC (area under the curve) score of ~64%, so model performance is quite low. Moreover, the ROC Curve below shows that as the true positive rate increases, so does the false positive rate, so, for every increase in the false positive rate, there is a greater increase in false alarms.
| Performance Metrics for Train Set | ||||
|---|---|---|---|---|
| Metric | Accuracy | Specificity | Sensitivity | F1-Score |
| Value | 0.65 | 0.59 | 0.95 | 0.73 |
| Performance Metrics for Test Set | ||||
|---|---|---|---|---|
| Metric | Accuracy | Specificity | Sensitivity | F1-Score |
| Value | 0.65 | 0.61 | 0.95 | 0.74 |
We are interested in seeing how the model performs on unseen data. Thus, we partition the data into a train-test split. Ideally, there are enough rows of data to conduct a three-way train-validation-test split such that the train-validation set becomes the development set. However, we are working with a smaller amount of data, so we are using a two-way split, where the training set (development set) is the larger portion of data (70-80%), and the remaining 30% is allocated to the test set. Anything can be done repeatedly to the development set (e.g., iteration, hyperparameterization, experimentation, etc.), as long as the test set remains uncontaminated (unseen). Once the model is finalized through the training set, it can be predicted on the remaining test set.